A cloroquina é um medicamento utilizado no Brasil desde os anos 1950. É indicada para o tratamento de várias doenças, como artrite reumatóide, lúpus e malária. A hidroxicloroquina é a versão mais "moderna" da droga, com efeitos colaterais mais leves.
Estas drogas vêm sendo usadas de forma experimental no Brasil e em outros países, apesar de não existirem testes clínicos suficientes para garantir que sejam eficazes ou seguras no tratamento da Covid-19.
Os efeitos colaterais podem incluir arritmia cardíaca e possíveis danos à visão e à audição. Por isso, a Fundação Oswaldo Cruz (Fiocruz) recomenda que sejam usadas com muito cuidado, pois podem ser letais em algumas circunstâncias. O difosfato de cloroquina (nome técnico da versão mais antiga da droga) faz parte de um conjunto maior de pesquisas relacionadas ao novo coronavírus.
Abaixo tem-se os 12 estudos autorizados até o dia 21 de abril de 2020 com a hidroxicloroquina, distribuídos entre os Estados Nacionais:
O boletim da Comissão Nacional de Ética em Pesquisa (CONEP) menciona 112 estudos sobre o vírus aprovados até 20 de abril de 2020. No gráfico acima mostra o número de estudos autorizados em cada Estado até a referida data. Diante, disso pode-se responder as questões abaixo:
a) Em São Paulo, qual o percentual de estudos em relação ao total de estudos autorizados até a data referida?
Para responder essa questão, devemos verificar que dos 112 estudos autorizados até a data, 60 deles estão sendo feitos no Estado de São Paulo. Como percentual é a parte de um todo, devemos efetuar o cálculo de divisão entre a parte de 60 pelo todo de 112, da seguinte maneira e obter o resultado:
Logo, temos 53,57 % dos estudos autorizados no Estado de São Paulo. É possível que se possa responder como certa de 54%, pois é um arredondamento do valor percentual mais próximo.
b) Qual o percentual dos Estados Nacionais que foram autorizados estudos que possuem apenas 01 estudo em evolução?
Como são 12 Estados Nacionais escolhidos e pelo gráfico 5 dos Estados possuem 01 estudo em evolução, calcula-se:
Logo, certa de 41,6% dos Estados possuem apenas 01 estudo em evolução.
c) Quais dos Estados possuem o número de 10% do número de estudos autorizados para o Estado de São Paulo?
Como para o Estado de São Paulo foram autorizados 60 estudos, e calculando 10% de 60:
10% x 60 = 0,10 x 6 = 6
Os Estados que possuem 6 estudos autorizados são Minas Gerais (MG) e Paraná (PR), como observado no gráfico.
Destes estudos autorizados, 24 são ensaios clínicos, que somam 12.508 pacientes. Além da cloroquina, também há dois ensaios com a nitazoxanida (comercializada como o vermífugo Annita); com corticoides, e até com a transfusão de plasma sanguíneo de pacientes convalescentes da Covid-19.
d) Pode-se perguntar: qual o percentual do número de estudos autorizados que são ensaio clínico?
E efetuando o cálculo, tem-se:
Logo, pode-se responder que certa de 21% dos estudos autorizados são ensaios clínicos.
ATENÇÃO: Não é recomendável tomar qualquer tipo de medicamento sem recomendação médica !!!
A Norma Operacional CNS/MS nº 001/2013, item 3.1, considera "protocolo de pesquisa como o conjunto de documentos, que pode ser variável a depender do tema, incluindo o projeto, e que apresenta a proposta de uma pesquisa a ser analisada pelo Sistema CEP-CONEP”.
Os ensaios clínicos são um conjunto de procedimentos de investigação e desenvolvimento de medicamentos, que são realizados para permitir que dados de segurança (ou mais especificamente, informações sobre reações adversas e efeitos adversos de outros tratamentos) e eficácia a recolher para as intervenções de saúde (por exemplo, drogas, diagnóstico, dispositivos, protocolos de terapia). Estes ensaios só podem ter lugar após informação satisfatória ser recolhida sobre a qualidade da segurança não-clínica, e as Autoridades de Saúde / Comissões de Ética aprovarem a realização dos ensaios no país em que o mesmo se está a realizar.
Referência: https://www.bbc.com/portuguese/geral-52360112
Definição: Um infográfico é uma apresentação de informações integradas em textos sintéticos com dados numéricos e elementos gráficos e visuais tais como fotografias, desenhos, diagramas estatísticos, gráficos etc.
1) Abaixo é apresentado um infográfico usando os dados do Suplemento Prática de Esporte e Atividade Física da PNAD 2015., produzido pelo IBGE (vamoscontar.ibge.gov.br), se referindo à população brasileira:
a) Segundo os resultados da pesquisa do gráfico acima, qual a porcentagem de pessoas de 15 anos ou mais que praticaram algum esporte ou atividade física no período de um ano?
Pelo infográfico, observando em total, vemos que 37,9 % da população acima de 15 anos praticam esporte ou atividade física.
b) O título genérico do infográfico da figura, a saber, “Quem mais pratica esportes e atividades físicas? - Percentual de pessoas de 15 anos ou mais que praticaram algum esporte ou atividade física-Brasil (2015)”, diz respeito à população brasileira de 15 anos ou mais ou à amostra coletada?
Pode-se agora, definir população e amostra. Em geral, a palavra população representa um conjunto de habitantes de um determinado lugar.
No entanto, em Estatística, população tem um sentido mais amplo e pode ser definida como o conjunto de todos os elementos com pelo menos uma característica em comum. Observe que é exatamente essa característica em comum que vai definir o universo (população) de uma pesquisa.
Assim, em Estatística, a população não precisa ser um conjunto de pessoas, pode ser o conjunto de parafusos fabricados por uma indústria, o conjunto de animais de certa espécie que vivem em uma região, todos os estudantes do ensino médio de um país, entre outros.
Amostra é um subconjunto não vazio da população. Por exemplo, quantidade de parafusos que um profissional necessita utilizar, uma espécie específica de animal que vivem numa região; estudantes de uma turma do ensino médio, entre outros.
No caso do nosso infográfico, a população da pesquisa é a população brasileira e os dados referem-se à toda população brasileira de 15 anos ou mais.
c) Com base nas recomendações médicas sobre a prática de atividades físicas para se ter boa saúde, como pode-se avaliar o resultado obtido na pesquisa para a população brasileira de 15 anos ou mais?
Não parece satisfatório. Vários estudos têm demonstrado que a prática de atividades físicas é fundamental para se ter boa saúde.
d) Considerando homens e mulheres separadamente, percebe-se alguma diferença com relação à prática de atividades físicas? Em caso afirmativo, descreva a(s) diferença(s) observada(s).
Sim. Entre os homens brasileiros de 15 anos ou mais, pouco mais de 40% praticam atividade física; enquanto esse percentual para mulheres brasileiras de 15 anos ou mais é pouco menor do que 35%.
e) Considerando as faixas etárias discriminadas no infográfico, percebe-se alguma diferença com relação à prática de atividades físicas? Em caso afirmativo, descreva a(s) diferença(s) observada(s).
Sim. Percebe-se uma diminuição dos percentuais de pessoas que praticam atividade física, conforme a idade aumenta. Na faixa de 15 a 17 anos temos mais de 50%, na faixa de 18 a 24 anos temos um pouco menos do que 50%, na faixa de 25 a 39 anos temos pouco mais de 40%, na faixa de 40 a 59 anos temos mais de 30% e na faixa 60 anos ou mais temos menos de 30%.
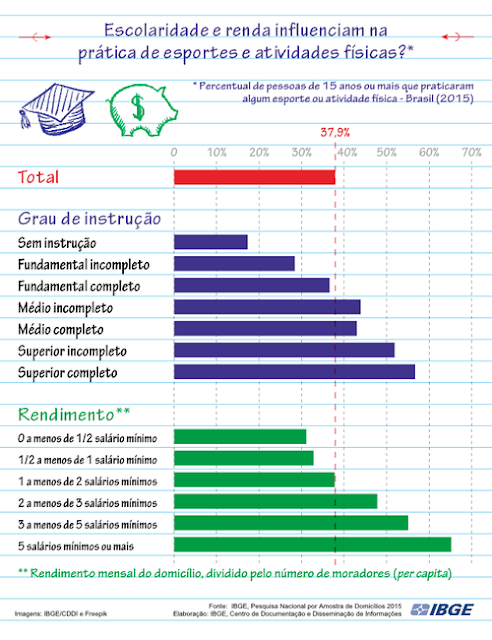
2) Outro infográfico usando os dados do Suplemento Prática de Esporte e Atividade Física da PNAD 2015., produzido pelo IBGE (vamoscontar.ibge.gov.br), mas agora questionando se escolaridade e renda influenciam na prática de esportes e atividades físicas?
a) Considerando os diferentes graus de instrução no infográfico acima, percebe-se alguma diferença com relação à prática de atividades físicas? Em caso afirmativo, descreva a(s) diferença(s) observada(s).
Sim, a porcentagem de pessoas de 15 anos ou mais que pratica atividade física cresce conforme o grau de instrução é maior.
b) Considerando as faixas de rendimento mensal per capita do domicílio, percebe-se alguma diferença com relação à prática de atividades físicas? Em caso afirmativo, descreva a(s) diferença(s) observada(s).
Sim, a porcentagem de pessoas de 15 anos ou mais que pratica atividade física cresce conforme a faixa de rendimento per capita é maior.
3) Outro infográfico usando os dados do Suplemento Prática de Esporte e Atividade Física da PNAD 2015., produzido pelo IBGE (vamoscontar.ibge.gov.br), mas agora questionando Quais os principais esportes praticados?
a) Qual foi a variável estudada no gráfico da figura?
Pode-se agora, definir elemento e variável estatística. Cada uma das unidades investigadas em um estudo estatístico é denominada um elemento.
Assim, cada parafuso investigado é um elemento na pesquisa de uma indústria de parafusos; cada paciente observado é um elemento numa pesquisa sobre efeitos de uma medicação; e cada domicílio e seus residentes são elementos na atividade do PNAD ou CENSO.
Cada característica observada de um elemento é uma variável estatística. Assim, a medida do diâmetro do parafuso é uma variável na pesquisa em uma indústria de parafusos, o tempo de cura da dor de cabeça é uma variável na pesquisa sobre os efeitos de uma medicação, nas pesquisas da PNAD ou no CENSO, estão presentes várias variáveis estatísticas de interesse do domicílio e de seus residentes tais como local, número de cômodos, número de residentes; sexo, idade e rendimento dos residentes, entre outras.
No infográfico acima temos como variável a modalidade de atividade física praticada.
b) A variável estudada tem respostas de que tipo: numéricas ou não numéricas?
Não numéricas: Futebol, Natação, entre outros.
c) Qual foi a resposta que apresentou a maior frequência?
Definindo frequência estatística como o número de vezes que o evento ocorreu em um experimento ou número de dados de cada variável em uma pesquisa ou estudo. Essas frequências são normalmente representadas graficamente em histogramas, como no infográfico acima.
E nesse infográfico a variável de maior frequência é o Futebol.
d) O que pode representar a resposta “Outros Esportes”?
Como as últimas modalidades discriminadas no gráfico apresentaram porcentagens muito pequenas (“ciclismo”, “ginástica rítmica e artística”, “lutas e artes marciais”, “voleibol, basquetebol e handebol”), cerca de 2%, a categoria outros esportes reuniu modalidades que ocorreram com porcentagens muito pequenas, não cabendo representá-las separadamente no gráfico. Observe que a última modalidade, antes de “outros esportes” já está reunida em mais de uma modalidade, a saber, “voleibol, basquetebol e handebol”.
4) Segundo os dados do Suplemento Prática de Esporte e Atividade Física da PNAD 2015., produzido pelo IBGE (vamoscontar.ibge.gov.br), o infográfico abaixo responde o questionamento: O poder público deve investir em atividades físicas ou esportivas?
a) Qual a porcentagem de pessoas de 15 anos ou mais que concorda com que o poder público deva investir em atividades físicas ou desportivas conforme o infográfico acima?
Observando o gráfico de setores, temos 73,3%.
b) Qual a opinião das pessoas de 15 anos ou mais que concordam que o poder público deve investir em atividades físicas ou esportivas com relação à prioridade de investimentos?
Entre as pessoas que acham que se devam priorizar investimentos em atividades físicas, 91,1% acha que o investimento deve ser para atividades físicas para as pessoas em geral, 8% acha que deve ser para a formação de atletas e, o restante (0,9%) respondeu outro tipo de prioridade.
c) Entre as pessoas de 15 anos ou mais que não concordam que o poder público deve investir em atividades físicas ou esportivas, que área elas entendem como prioritária?
Entre as pessoas que não concordam que o poder público deve investir em atividades físicas, 57,8% acham que a prioridade deve ser Saúde, 21,3% acham que a prioridade deve ser Segurança, 16,5%, acham que a prioridade deve ser Educação e, o restante (4,4%) respondeu outros tipos de prioridade.
d) Podemos afirmar que 57,8% das pessoas de 15 anos ou mais defendem que o poder público deve investir em Saúde?”
Não, de fato, são 57,8% de 14,7% o que dá cerca de 8,5% das pessoas de 15 anos ou mais.
Atividades:
1) Ao entrar na sala de aula após o recreio, Edite encontrou o quadro abaixo escrito no quadro negro, com alguns dados apagados. Esse quadro se refere às quantidades e porcentagens de alunos da classe que torcem pelos times: Botafogo, Flamengo, Fluminense, Vasco.
Sabendo que todos os alunos dessa classe torcem por um desses times, Edite concluiu que os dados que faltam nesse quadro são:
(A) 16 e 30%. (B) 19 e 31%. (C) 24 e 75%. (D) 76 e 25%.
2) A tabela abaixo mostra o resultado de uma pesquisa realizada com 1.200 jovens de uma escola, para saber o que eles fazem para evitar a acne. Cada um desses jovens utiliza apenas um método.
Quantos desses jovens lavam o rosto várias vezes ao dia?
(A) 32 (B) 60 (C) 276 (D) 384
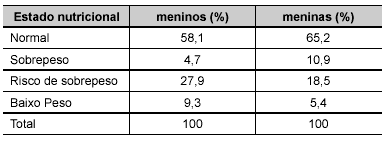
Considerando que o número de meninos e meninas que participou dessa pesquisa foi o mesmo, qual é o percentual de adolescentes com sobrepeso?
(A) 4,7%. (B) 10,9%. (C) 15,6%. (D) 46,4%.
4) “O telefone celular, antes tão mal visto no ambiente escolar, vai ocupando cada vez mais espaço na sala de aula: em 2016, 52% das escolas utilizavam o aparelho em atividades com os alunos. É o que aponta a pesquisa TIC Educação 2016, do Centro de Estudos sobre as Tecnologias da Informação e da Comunicação (CETIC)”. Numa pesquisa foram coletados dados de 10.000 estudantes e o resultado foi apresentado no gráfico abaixo:
O gráfico é apresentado com valores percentuais e a resposta foi computada como o dispositivo que ele mais utiliza:
a) Que variável foi analisada nesse gráfico e qual a sua classificação (numérica ou não numérica) ?
b) Que tipo de gráfico foi usado para representar as respostas dessa variável ?
c) Esse tipo de amostra poderia ser apresentado na forma de gráfico de setores? Se possível, como ficaria seu esboço?
d) Quantos alunos pesquisados utilizam o celular para acessarem a Internet?
e) Quantos alunos pesquisados utilizam o videogame para acessarem a Internet?
5) O gráfico a seguir mostra quanto tempo um estudante gasta com suas atividades durante o dia.
a) Qual o percentual do tempo gasto com “Outras Atividades”?
b) Quanto tempo esse estudantes leva na escola por dia?
c) É possível determinar a quantidade de horas de sono?
d) Qual quantidade de horas gastas pelo estudante com “Outras Atividades” em um dia?
6) Após serem medidas as alturas dos alunos de uma turma, elaborou-se o seguinte histograma:
a) Qual o número total de alunos na turma?
b) Qual o percentual de alunos têm altura de 1,70m a 1,80m?
c) Qual o percentual de alunos possui estatura mais baixa, entre 1,60m a 1,70m?
d) Como ficariam os dados percentuais das alturas dos alunos em um gráfico de setores?
7) Um pesquisador da área de Saúde estudou os efeitos da obesidade sobre a população de uma comunidade.
Para isso, calculou o índice de massa corporal (IMC) dos 80 integrantes dessa comunidade e dividiu-os em 6 grupos. O gráfico, abaixo, mostra os resultados obtidos nessa pesquisa.
(A) 25%. (B) 36%. (C) 45%. (D) 55%.
8) Na turma de Sara, fez-se uma pesquisa sobre o número de alunos que já viajaram de avião. Os resultados foram registrados no gráfico abaixo.
De acordo com os dados desse gráfico, constata-se que:
(A) 30% dos alunos nunca viajaram de avião.
(B) 30% dos alunos viajaram de avião duas vezes.
(C) 40% dos alunos viajaram de avião apenas uma vez.
(D) 80% dos alunos já viajaram de avião.
9) O quadro, abaixo, mostra o percentual dos votos válidos obtido por quatro candidatos à presidência da República.
Qual dos gráficos, abaixo, melhor representa esses dados?
Em qual desses círculos a parte colorida na cor cinza representa 25% da região circular?
11) A pizza é, sem dúvida, o alimento preferido de muitos brasileiros. Estima-se que o consumo diário no Brasil seja de 2 milhões de pizzas, sendo o Estado de Rio de Janeiro responsável por 40% desse consumo. O gráfico abaixo exibe a preferência do consumidor fluminense em relação aos tipos de pizza.
a) Quantas pizzas são consumidas diariamente no Brasil, fora do Estado do Rio de Janeiro?
b) Quantas pizzas de mozarela e de calabresa são consumidas diariamente no Estado do Rio de Janeiro?
12) Na porte de um cinema foram entrevistadas mil pessoas, sobre o estilo de filme preferido e o resultado da pesquisa foi apresentado no gráfico abaixo:
a) Quantos dos entrevistados preferem filmes de ação?
b) Quantas pessoas preferem o drama?
c) Fazendo-se um sorteio entre os participantes da entrevista, qual a probabilidade dessa pessoa ter preferência por filmes de terror?
13) O gráfico, abaixo, mostra a distribuição dos 60 alunos de uma turma de terceira série do Ensino Médio de acordo com a preferência por quatro áreas de conhecimento.
Quantos alunos preferem as ciências humanas?
(A) 9 (B) 12 (C) 18 (D) 21
De acordo com esse gráfico, o percentual de idosos nessa cidade é:
(A) 1,88%. (B) 18,8%. (C) 20%. (D) 25%.
15) Em uma escola foi realizada uma pesquisa sobre a preferência de 400 alunos quanto ao gênero de filmes mais assistidos. Os resultados dessa pesquisa estão representados no gráfico abaixo.
Nesse grupo de 400 alunos, entre os que preferem comédia, 40 são mulheres.
Quantos homens preferem comédia?
(A) 40. (B) 80. (C) 120. (D) 160.
16) Em uma pesquisa onde 3.000 pessoas foram entrevistadas com o seguinte questionamento: O que leva as pessoas a se mudarem para os condomínios fechados fora das grandes cidades? As respostas foram organizadas no gráfico a seguir, após análise do gráfico, pode-se afirmar que:
(A) 360 pessoas mudam devido ao conforto.
(B) 660 pessoas mudam devido à tranquilidade.
(C) 840 pessoas mudam devido ao espaço.
(D) 1.140 pessoas mudam devido à segurança.
17) (ENEM 2015) O polímero de PET (Politereftalato de Etileno) é um dos plásticos mais reciclados em todo o mundo devido à sua extensa gama de aplicações, entre elas, fibras têxteis, tapetes, embalagens, filmes e cordas. Os gráficos mostram o destino do PET reciclado no Brasil, sendo que, no ano de 2010, o total de PET reciclado foi de 282 kton (quilotoneladas).
(A) 16 (B) 22,9 (C) 32 (D) 84,6 (E) 106,6
18) O gráfico abaixo reflete a evolução dos casos de Coronavírus registrados por dia no período do final de fevereiro até o início de maio.
a) Entre os dias 26 de abril a 29 de abril, houve um crescimento ou decrescimento diário da curva de contaminação?
b) Em 1º de maio a curva de contaminação estava na sua região de crescimento ou decrescimento em relação aos dias anteriores?
c) Em que dias houveram registros de cerca de 3.300 confirmações de casos?
d) No gráfico, o maior valor de casos confirmados num dia foi de mais de 7.000 casos no dia 30 de abril. Sabendo que até essa data foram confirmados um total de 700.000 casos de Coronavírus no Brasil. Qual o percentual de casos nesse dia em relação ao total de contaminações?
19) (ENEM 2016) O cultivo de uma flor rara só é viável se do mês do plantio para o mês subsequente o clima da região possuir as seguintes peculiaridades: a variação do nível de chuvas (pluviosidade), nesses meses, não for superior a 50mm a temperatura mínima, nesses meses, for superior a 15°C; ocorrer, nesse período, um leve aumento não superior a 5°C na temperatura máxima.
Um floricultor, pretendendo investir no plantio dessa flor em sua região, fez uma consulta a um meteorologista que lhe apresentou o gráfico com as condições previstas para os meses seguintes nessa região.
20) (ENEM-2017) Num dia de tempestade, a alteração na profundidade de um rio, num determinado local, foi registrada durante um período de 4 horas. Os resultados estão indicados no gráfico de linhas. Nele, a profundidade h, registrada às 13 horas, não foi anotada e, a partir de h, cada unidade sobre o eixo vertical representa um metro.

Foi informado que, entre 15 horas e 16 horas, a profundidade do rio diminuiu em 10%.
Às 16 horas, qual é a profundidade do rio, em metro, no local onde foram feitos os registros?
(A)18 (B) 20 (C) 24 (D) 36
Aprofunde-se:
1) Leia a manchete abaixo:
“Produção de lixo por morador cresce 9% no município do Rio de Janeiro.”
Segundo relatório emitido pela COMLURB, Companhia Municipal de Limpeza Urbana, em 2015, cada habitante do município do Rio de Janeiro gerou aproximadamente 0,5 kg (500 g) de lixo por dia.
De acordo com essas informações, qual foi a produção diária de lixo por habitante na data da pesquisa?
(A) 1,2 kg (B) 545 g (C) 0,45 kg (D) 600 g
2) Em uma indústria, trabalham 720 funcionários, dos quais 450 são homens. Nessa indústria, o percentual de funcionários do sexo feminino é:
(A) 27%. (B) 37,5%. (C) 55%. (D) 62,5%.
3) Um grupo de 50 pessoas participou de uma excursão. Desse total, 60% são mulheres. Dentre as mulheres, 20% são idosas. Nesse grupo, há quantas mulheres idosas?
(A) 6. (B) 10. (C) 30. (D) 40.
4) O Ministério da Saúde começou, em abril de 2019, uma nova campanha para imunizar a população contra a gripe Influenza H1N1. No “Dia D”, que marcou o início da campanha, a Secretaria Municipal do Rio de Janeiro – MG vacinou 20.000 pessoas, o que corresponde a 20% da meta a ser atingida.
Quantas pessoas ainda precisam ser vacinadas para se atingir a meta da Secretaria?
(A) 14 400. (B) 18 000. (C) 72 000. (D) 90 000.
5) Segundo informação da Divisão de Saúde da Universidade do Estado do Rio de Janeiro, em abril de 2019, foram registrados 200 casos de conjuntivite. Foram 85 casos nas três primeiras semanas e 63 casos na última semana. Qual foi, aproximadamente, o percentual de casos registrados na última semana em relação ao total do mês?
(A) 26,0%. (B) 40,0%. (C) 62,3%. (D) 66,0%.
6) Segundo orientação dos médicos, para se evitar lesões na coluna, o peso de uma mochila, com o material escolar que ela contém, não deve ultrapassar 10% do peso do estudante que a transporta. Tito pesou sua mochila vazia e verificou que ela pesava 700 g. Sabendo que Tito pesa 42 kg, qual é o peso máximo que ele deve transportar dentro dessa mochila, de modo a evitar lesões na coluna?
(A) 3,5 kg (B) 4 kg (C) 5,2 kg (D) 7 kg