Relação de Euler

Sólidos Geométricos

O prisma retangular, o cubo, o cilindro, o cone, a pirâmide são formas geométricas espaciais que aparecem com frequência em nosso cotidiano. Abaixo temos exemplos junto com suas planificações.

Anote as características encontradas nesses sólidos:

·        Prisma Retangular (Paralelepípedo):

Número de faces: _________ Número de vértices: ________ Número de arestas: ________

·        Cubo (Prima Quadrangular):

Número de faces: _________ Número de vértices: ________ Número de arestas: ________

·        Prisma Triangular

Número de faces: _________ Número de vértices: ________ Número de arestas: ________

      

Pirâmide Triangular   Número de faces: _________ Número de vértices: ________ Número de arestas: ________

 

Pirâmide Quadrangular

Número de faces: _________ Número de vértices: ________ Número de arestas: ________

Pirâmide Pentagonal   Número de faces: _________ Número de vértices: ________ Número de arestas: ________

Pirâmide Hexagonal

Número de faces: _________ Número de vértices: ________ Número de arestas: ________

Observe que uma pirâmide é caracterizada pelo polígono que forma sua base.

Apresente suas características comuns:

 As características geométricas de uma pirâmide são:

• a base é um polígono;

• as faces laterais são triangulares.

• o número de faces laterais é o número de lados do polígono da base.

Atividade: Em um cubo estão desenhadas em suas seis faces formas planas circular, quadrada, triangular, pentagonal, hexagonal e estrela.

 

Veja o desenho desse cubo em três posições diferentes:

Descubra quais são as formas planas que estão nas faces opostas.

 

Veja algumas das principais características de um prisma:

 • as bases de um prisma são polígonos;

• a base superior e a base inferior de um prisma qualquer são iguais;

• se a base é um polígono regular (aquele que tem todos os lados e todos os ângulos congruentes), diz-se que o prisma é regular;

• as faces laterais de um prisma reto são retangulares.

Um prisma qualquer, seja reto, seja oblíquo, tem sempre duas bases (inferior e superior) que são polígonos, e tem faces, vértices e arestas.

Toda forma geométrica tridimensional que possui esses três elementos (faces, vértices e arestas) são denominados de poliedros.  

         Em geral, poliedros são conceituados como sólidos geométricos delimitados por faces planas poligonais.

Desse ponto de vista, os prismas e as pirâmides são poliedros, pois eles são sólidos geométricos delimitados por faces planas quadradas, retangulares, triangulares, pentagonais, hexagonais, entre outros.

Agora reflita: O que a bola de futebol tem a ver com poliedros? A princípio nada a ver, pois a bola de futebol, aparentemente, é um outro tipo de sólido tridimensional, que é denominado de corpos redondos.  Além da forma geométrica da bola chamada de esfera, destacam-se como corpos redondos o cone e o cilindro.    Atividade:  1) Quais dos objetos abaixo a seguir têm forma de poliedro e quais corpos redondos?    2) São semelhantes a prismas e a corpos redondos, respectivamente:        (A) Casquinha de sorvete e pirâmide.        (B) Caixa de fósforos e caderno.        (C) Casquinha de sorvete e canudo.        (D) Pirâmide e Canudo.        (E) Caixa de fósforos e chapéu de festas. 3) Quais são os sólidos geométricos representados pelas  planificações abaixo?   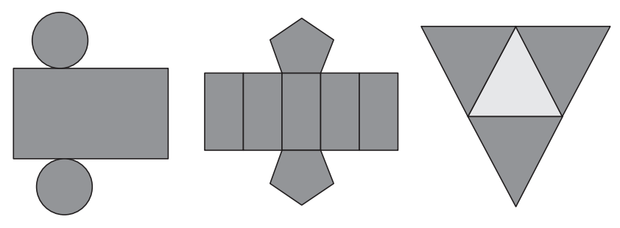4) A forma geométrica representada pela figura abaixo  é:                                       (A) tetraedro               (B) pirâmide retangular              (C) prisma quadrangular reto                   (D) prisma triangular reto 5) A figura abaixo representa a planificação de um sólido geométrico. .                                 O sólido planificado é:       (A) uma pirâmide de base hexagonal.       (B) um prisma de base hexagonal.       (C) um paralelepípedo.       (D) um hexaedro.       (E) um prisma de base pentagonal 6) A figura, abaixo, mostra uma embalagem de presente que Bruno desmontou. Como era essa embalagem antes de ser desmontada? 7) Observe os objetos tridimensionais representados nas figuras abaixo. Esses objetos têm, respectivamente, as formas de:     (A) cilindro, prisma e paralelepípedo retângulo.     (B) cilindro, pirâmide e prisma.     (C) cone, prisma e paralelepípedo retângulo.     (D) cone, pirâmide e prisma quadrangular. Relação de Euler O matemático suíço Leonhard Euler (1707-1783) fez uma das grandes descobertas da Matemática e, em sua homenagem, ela recebeu o nome de relação de Euler. A fórmula de Euler relaciona o número de faces, arestas e vértices de um poliedro, e é verdadeira para todos eles. O que impressiona nessa fórmula é sua simplicidade. Euler observou que a soma do número de faces com o número de vértices é igual ao número de arestas acrescido de 2.   Atividades: 1) Um poliedro convexo é constituído por 25 arestas e 15 faces. Quantos vértices possui esse poliedro?   2)  Um poliedro convexo de 7 faces possui 10 vértices. Quantas arestas possui esse poliedro? 3) Qual o número de faces de um poliedro convexo constituído por 16 vértices e 24 arestas? 4) (SAEB) Ao passar sua mão direita por todos os vértices e arestas de um poliedro, somente uma vez, um deficiente visual percebe que passou por 8 vértices e 12 arestas. Conclui-se que o número de faces desse poliedro é igual a:           (A) 20          (B) 12        (C) 8       (D) 6       (E) 4   5) Uma caixa no formato de um poliedro precisa ser reforçada com 1 parafusos em cada vértice, um revestimento de metal nas suas 7 faces e uma aplicação de uma cola especial em todas as 15 arestas. A quantidade necessária de parafusos será igual a:          (A) 72.     (B) 66.      (C) 24.     (D) 30.      (E) 10. 6) Um poliedro convexo é constituído por 20 arestas, e seu número de vértices é igual ao número de faces. Quantos vértices possui esse poliedro? 7) Um poliedro convexo possui 12 faces pentagonais. Quantas arestas esse poliedro possui? E quantos vértices?    8) Um poliedro convexo é  constituído por três faces triangulares, cinco quadrangulares e sete pentagonais. Quantas arestas possui esse poliedro? E quantos vértices?     Poliedros de Platão 1) Utilizando a relação de Euler, complete a tabela abaixo:   Sólidos de Platão Vértices Faces Arestas Tetraedro 4   6 Hexaedro   6 12 Octaedro 6 8   Dodecaedro 20 12   Icosaedro 12   30   2) Um poliedro regular possui 30 arestas e 20 vértices. Quantas faces possui esse poliedro? E qual é o nome desse poliedro?   3) Um poliedro convexo é formado por 12 faces pentagonais e 20 faces hexagonais, todas regulares. Quantos vértices possui esse poliedro?  Da propriedade 1 de poliedros convexos sabemos que: Agora, como conhecemos o número de arestas e o número de faces, podemos utilizar a relação de Euler: 4) Um poliedro convexo tem 8 faces, sendo 4 triangulares e 4 quadrangulares. Quantos são os seus vértices?        (A) 8     (B) 9     (C) 14    (D)28    (E) 16   5) Arquimedes descobriu um poliedro convexo formado por 12 faces pentagonais e 20 faces hexagonais, todas regulares. Esse poliedro inspirou a fabricação da bola de futebol que apareceu pela primeira vez na Copa do Mundo de 1970.     a) Quantas arestas possui esse poliedro? _______________ b) Quantos vértices possui esse poliedro? ______________ 6) O poliedro convexo ilustrado abaixo tem 32 faces, sendo 20 faces triangulares e 12 faces pentagonais. Quantos são os seus vértices? Aprofunde-se:   Sólidos de Platão: http://caetanomatematica.blogspot.com/2018/10/os-solidos-de-platao-os-solidos-de.html  Sólidos de Arquimedes: http://caetanomatematica.blogspot.com/2018/10/os-solidos-de-arquimedes-treze.html