É possível ouvirmos notícias como essas abaixo:
a) Foi publicada a previsão do tempo, indicando que a probabilidade de chover amanhã na região onde você mora e estuda é de 30%.
Que decisão você tomaria com base nessa previsão: levar ou não um guarda-chuva para a escola? Por quê? Como você interpreta essa previsão?
b) Um estudo na área de Saúde
indicou que a probabilidade de uma pessoa vir a ter o Diabetes é 10%. Isso
significa que ao acompanhar um grupo de 500 pessoas, 50 delas terão Diabetes?
Por quê?
Explorar a noção de probabilidade serve
para, apresentar uma teoria matemática útil para calcular probabilidades de
eventos associados a experimentos
aleatórios ou fenômenos aleatórios, isto é, experimentos cujos resultados finais são conhecidos somente após a
realização dos mesmos.
Por Por
exemplo,
a) o número de likes que você
irá receber no período de 24h após a sua postagem em uma rede social;
b) a quantidade de metros
cúbicos de gás consumida na sua residência no primeiro semestre do próximo ano;
c) o tempo, contado a partir
de hoje, que a lâmpada do seu quarto levará para queimar;
d) o número de quilowatts
consumidos na sua residência no próximo mês.
Para explicar fenômenos
aleatórios como exemplificados nos itens acima, usamos modelos matemáticos não determinísticos chamados modelos probabilísticos. Neste caso,
mesmo conhecendo algumas condições, não é possível determinar qual será o
resultado antes da realização do experimento.
Nesse estudo analisaremos as
características extraídas dos dados aleatórios amostrais a fim de revelar como
a Estatística nos auxilia a descrever as regularidades de ocorrências de
determinados eventos aleatórios.
Vejamos exemplos eventos aleatórios probabilísticos:
1) Probabilidade clássica
a) De um grupo de 10 estudantes, um será sorteado para ser o representante de turma. Como são 4 meninas e seis meninos, decidiu-se, para fazer o sorteio, representar as meninas por cartões ilustrados com triângulos e os meninos por cartões ilustrados com círculos. Os cartões foram colocados numa caixa e um será sorteado. Qual é a probabilidade (e chance) de ser escolhida uma menina como representante de turma? Por quê?
Nesses tipos de itens pode-se pensar que cada resultado possível tenha a mesma chance de ocorrer. Assim temos,
A probabilidade é 4 / 10 (“4 para 10”), pois
são 10 cartões e quatro deles apresentam “triângulos” que representam meninas e
assim 40% de chance de ser escolhida uma menina.
b) Numa rua há 10 casas. O
número de moradores por casa está representado na figura abaixo. Suponha que
você irá escolher ao acaso uma casa desta rua. Qual é a probabilidade de que a casa escolhida
tenha exatamente 4 moradores? Por quê?
Daí, temos:
A probabilidade é 2 / 10 (“2 para 10”), pois são 10 casas e duas delas têm exatamente 4 moradores e assim 20% de ser escolhida uma casa com exatamente 4 moradores.
c) Qual é a probabilidade de
que a casa escolhida tenha mais de 4 moradores? Por quê?
A probabilidade é 4 / 10 (“4 para 10”), pois são 10 casas e quatro delas têm mais de 4 moradores, e assim 40% de ser escolhida uma casa com mais de 4 moradores.
2) Probabilidade frequentista
a) Suponha que você tenha
lançado uma moeda 20 vezes e que tenha observado a face “cara” 19 vezes e a
face “coroa” uma vez. Se você lançar esta moeda mais uma vez, qual é a
probabilidade (chance) de a face voltada para cima resultar em “cara”? Por quê?
Nesses itens o objetivo é determinar
probabilidades, usando o enfoque frequentista de probabilidade, atribuindo como
resposta a frequência relativa de ocorrência do evento.
Daí, temos:
Com uma probabilidade de 19 / 20 e 95% de
chance de ocorrer “cara”; que corresponde à frequência relativa de caras
obtidas nos 20 lançamentos.
Outras respostas podem ser consideradas neste
item, dependendo dos parâmetros
escolhidos, por exemplo, ½ = 50%, supondo-se,
apesar das evidências em contrário, que a moeda é honesta; ou calculando-se uma
média entre a frequência de caras observadas e a frequência esperada, supondo
que a moeda é honesta
e assim tendo 0,725 = 72,5% de chance de ocorrer
“cara”.
b) Suponha que um bebê tenha
nascido na maternidade mais próxima de sua casa na manhã de hoje. Qual é a
probabilidade de que este bebê seja um menino? Por quê?
Uma resposta possível é ½ = 0,5
= 50%, pois da experiência é possível verificar que meninas e meninos
nascem na mesma proporção.
c) A pesquisa TIC Educação 2016, do Centro de Estudos sobre as Tecnologias da Informação e da Comunicação (CETIC), coletou dados de cerca de 11 mil estudantes do segundo segmento do Ensino Fundamental e do Ensino Médio. Entre várias informações, verificou-se que cerca de 8.500 estudantes usam smartphones como seu principal meio de acesso à internet. A pesquisa aconteceu entre agosto e dezembro de 2016.”
(Leia reportagem publicada no G1.com.br).
Qual é a probabilidade de
que um estudante de Ensino Fundamental II ou Médio, escolhido ao acaso, use
como seu principal meio de acesso à internet um smartphone, usando os dados
dessa pesquisa? Por quê?
Assim temos 77,2% de probabilidade desse estudante
escolhido utilizar o smartphone, pois 8.500 estudantes de 11 mil responderam
que esse é o seu principal meio de acesso à internet na pesquisa realizada e
supondo que a pesquisa represente bem o comportamento na população de todos os
estudantes de Ensino Fundamental II e Médio.
3) Probabilidade subjetiva
a) Qual é a probabilidade de
que o Brasil se classifique na fase de grupos na próxima Copa do Mundo que irá
competir?
Nesses itens o objetivo é determinar
probabilidades, usando o enfoque subjetivo da probabilidade. Certos eventos são
únicos e não podem ser reproduzidos, mas por serem aleatórios, faz sentido
atribuir a eles probabilidades. As respostas aqui dependerão da experiência e
objetivos de cada um. As perguntas neste bloco têm o objetivo de estimular a
discussão sobre o conceito de probabilidade.
Uma resposta possível é maior do que 0,5 (50%),
pois o Brasil, além de ser o único país a ter participado de todas as Copas do
Mundo até a Copa de 2018, classificou-se na fase de grupos nas últimas 9
edições desse campeonato.
b) Qual é a probabilidade de
que daqui a 8 anos você tenha concluído um curso de nível superior?
A resposta dependerá de cada aluno. Por
exemplo, se for um um bom aluno do Ensino Médio que pretende cursar Engenharia,
curso que dura cinco anos, uma resposta possível seria uma probabilidade maior
do que 0,5 (50%). Por outro lado, se for um aluno que tem outros planos e não
pretende cursar o nível superior, uma resposta possível seria uma probabilidade
menor do que 0,5 (50%).
c) Qual é a probabilidade de
que você esteja casado(a) aos 25 anos?
A resposta dependerá de cada um. Uma
possibilidade nesse caso, quando não se sabe nada, é atribuir uma probabilidade
0,5 (50%).
Observação: A razão pela qual
usamos 0,5 (50%) como valor de comparação para avaliar probabilidades se dá
pelo fato de ser exatamente o centro da escala da probabilidade que varia de 0
a 1 (0 a 100%). Assim, se temos a percepção de que é mais provável que certo
evento ocorra do que ele não ocorra, atribuímos a ele uma probabilidade maior
do que 0,5 (50%). Por outro lado, se temos a percepção de que é menos provável
que certo evento ocorra do que ele não ocorra, atribuímos a ele uma
probabilidade inferior a 0,5 (50%). Se temos a percepção de que não existe
favorecimento entre a ocorrência ou não de certo evento, ou mesmo se não
sabemos nada sobre ele, atribuímos a ele uma probabilidade 0,5 (50%).
Revendo e Resumindo o Conceito de Probabilidade
No início do século XX, o matemático
russo Kolmogorov, estabeleceu regras básicas para a probabilidade que
independem da interpretação adotada, possibilitando assim, a construção de uma
teoria matemática de probabilidade.
De maneira simplificada, essas regras
básicas serão apresentadas a seguir.
Seja S um espaço amostral.
Uma probabilidade é uma função P que
associa a cada subconjunto de S (evento) um número real, tal que:
a) ela é sempre um número não
negativo,
b) a probabilidade do evento certo é
igual a 1 e,
c) dados dois eventos disjuntos, a
probabilidade da união dos dois é dada pela soma das probabilidades
individuais.
Em símbolos, essas regras podem ser apresentadas da seguinte forma:
a) P(A) ≥ 0 qualquer que seja A ⊂
S,
ou seja, a probabilidade de qualquer evento A é um número
não-negativo.
b) P(S) = 1, ou seja, a probabilidade
do evento certo é igual a 1.
c) Se A, B ⊂
S com A e B eventos
disjuntos (A ∩ B=∅), então P(A ∪
B)
= P(A) + P(B).
Atividades:
1) Em uma escola de Ensino
Médio há dois turnos: manhã e tarde. No turno da manhã há 450 alunos e, no
turno da tarde, 350 alunos. Os professores de Educação Física realizaram um
censo para saber se os alunos da escola praticavam algum tipo de atividade física
regular fora do período escolar. A pergunta principal do questionário da
pesquisa foi:
Qual é a sua atividade física principal fora do período escolar? Marque
apenas uma opção.
( ) Não pratica ( ) Futebol ( ) Natação ( ) Outra
Na tabela a seguir estão os resultados obtidos:
Um aluno desta escola será escolhido ao acaso.
Considere os eventos:
A: “o aluno escolhido não pratica atividade física”;
B: “o aluno escolhido pratica Futebol como atividade física
principal”;
C: “o aluno escolhido pratica natação” e
D: “o aluno pratica outro tipo de atividade física principal”.
Determine a probabilidade de cada um desses eventos.
Calculando P(A), como o total dos que não
praticam esporte é 270 e o número total de alunos é 800, então:
(...)
2) (ENEM-2005) As 23 ex-alunas de uma turma que
completou o Ensino Médio há 10 anos se encontraram em uma reunião comemorativa.
Várias delas haviam se casado e tido filhos. A distribuição das mulheres, de acordo
com a quantidade de filhos, é mostrada no gráfico abaixo.
(A) 1/3 (B) 1/4 (C) 7/25 (D) 7/23
RESPOSTA: Alternativa C
3) Imagine que tenha sido apresentado um documentário sobre terremotos, no qual é dito com que frequência ocorrem e como podem ser previstos. Nesse documentário, um geólogo afirmou: “nos próximos 20 anos, a probabilidade de um terremoto acontecer na cidade de Zed é de duas em três”.
Qual das sentenças a seguir reflete o significado da afirmação feita pelo geólogo?
(A) Como (2/3) x 20 ≈ 13,323; então entre 13 e 14 anos a partir de agora, ocorrerá um terremoto na cidade de Zed.
(B) Como 2/3 é maior do que 1/2, temos certeza de que ocorrerá um terremoto na cidade de Zed em algum momento nos próximos 20 anos.
(C) A probabilidade de ocorrer algum terremoto na cidade de Zed em algum momento nos próximos 20 anos é maior do que a probabilidade de ele não ocorrer.
(D) Não se pode dizer sobre o que irá acontecer, pois ninguém sabe quando um terremoto ocorrerá.
4) Para dado dia, a previsão do tempo afirma que, das 12h às 18h, a chance de ocorrência de chuva é de 30%.
Assinale a alternativa que corresponde à melhor interpretação dessa previsão do tempo.
(A) Em 30% da área à qual a previsão se refere haverá chuva.
(B) Em 30% de 6 horas, ou seja, durante o total de 108 minutos, haverá chuva.
(C) Em relação às pessoas da área à qual a previsão se refere, pode-se afirmar que 30 a cada 100 pessoas pegarão chuva.
(D) Se a mesma previsão fosse dada para 100 dias, em cerca de 30 desses 100 dias haveria chuva.
5) Três modelos de aparelhos de ar condicionado I, II e III, de diferentes potências são produzidos por determinado fabricante. Uma consulta sobre intenção
de troca de modelo foi realizada com 1.000 usuários desses produtos. A seguir estão indicados os tipos de modelos que os usuários possuem e se eles pretendem mudar para outro modelo ou não.
Dos 400 que possuem o modelo I, 50 não pretendem mudar de modelo, 150 pretendem mudar para o II e 250 para o III.
Dos 400 que possuem o modelo II, 100 não pretendem mudar e 300 pretendem mudar para o III.
E, dos 200 que possuem o modelo III, nenhum deles tem intenção de mudar.
Escolhendo-se aleatoriamente um dos usuários consultados, a probabilidade de que ele não pretenda trocar seu modelo de ar condicionado é:
(A) 20% (B) 35% (C) 40% (D) 65%
6) O diretor de um colégio leu numa revista que os pés das mulheres estavam aumentando. Há alguns anos, a média do tamanho dos calçados das mulheres era de 35,5 e, hoje, é de 37,0. Embora não fosse uma informação científica, ele ficou curioso e fez uma pesquisa com as funcionárias do seu colégio, obtendo o quadro a seguir:
Escolhendo uma funcionária ao acaso e sabendo que ela tem calçado maior que 36, qual a probabilidade de ela calçar 38?
7) Numa pequena ilha, há cem pessoas que
trabalham na única empresa ali existente. Seus salários (em moeda local) têm a
seguinte distribuição de frequências:
Dessa situação é correto, dizer:
(A) A
média aritmética dos salários é de $ 100,00.
(B)
Conhecendo-se uma dessas pessoas, a probabilidade dela receber $ 150,00 é 1/10.
(C)
Conhecendo-se uma dessas pessoas a probabilidade de ela não receber $ 50,00 é
3/10.
(D) A
mediana e a moda dos salários são números distintos entre si.
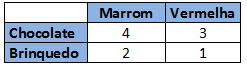
8) Durante o recreio, a professora colocou sobre a mesa dois saquinhos: um marrom e outro vermelho. Dentro desses saquinhos havia “bolas-surpresa”, indistinguíveis entre si, umas contendo chocolate e outras, brinquedo. A tabela a seguir apresenta a quantidade de bolas de cada tipo nos dois saquinhos:
Dessa situação é correto afirmar:
(A) Um aluno retira, ao acaso, uma bola do saquinho vermelho, então a probabilidade de essa bola conter chocolate é de 3/4.
(B) Um aluno retira, ao acaso, uma bola do saquinho vermelho, então a probabilidade de essa bola conter brinquedo é de 3/4.
(C) Um aluno retira, ao acaso, uma bola do saquinho marrom, então a probabilidade de essa bola conter chocolate é de 1/3.
(D) Um aluno retira, ao acaso, uma bola do saquinho marrom, então a probabilidade de essa bola conter brinquedo é de 2/3.
Sorteando uma bola, podemos, afirmar que:
(A) A probabilidade da bola não ser branca é 5/6 e a probabilidade dela ser verde é 1/12.
(B) A probabilidade da bola não ser azul é 1/6 e a probabilidade dela ser vermelha é 1/3.
(C) A probabilidade da bola ser amarela é a menor probabilidade em relação a ser as outras bolas.
(D) A probabilidade da bola ser verde é a maior probabilidade em relação a ser as outras bolas.
10) O quadro, abaixo, mostra o número de alunos em três cursos da Faculdade de Engenharia.
Um desses
alunos foi sorteado para fazer estágio numa empresa. Sabendo-se que a pessoa
sorteada faz Engenharia de Produção, qual é a probabilidade de ser uma mulher?
(A) 5/8 (B) 5/11 (C) 25/112 (D) 55/112
11) As áreas construídas, medidas em metros quadrados, de vinte residências de certa região estão distribuídas no gráfico abaixo, com os dados das áreas e o número de casas com cada área.
12) Foi realizado um levantamento nos
200 hotéis de uma cidade, no qual foram anotados os valores, em reais, das
diárias para um quarto padrão de casal e a quantidade de hotéis para cada valor
da diária.
Os valores das diárias foram: A =
R$ 200,00; B = R$ 300,00; C = R$ 400,00 e D = R$ 600,00. No gráfico, as áreas
representam as quantidades de hotéis pesquisados, para cada valor da diária.
a) Qual o número de hotéis que têm diária de R$ 600,00?
b) O casal Romeu e Julieta, passando o final de semana nessa
cidade, se hospedou num deles, qual a probabilidade deles terem se hospedado no
que tem valor de R$ 300,00?
c) No gráfico de setor, qual o
percentual aplicado para cada um dos setores?
Aprofunde-se:



















Nenhum comentário:
Postar um comentário