A palavra logaritmo, criada por John Napier (1550-1617), significa
expoente.
Considere uma potência qualquer de base positiva diferente de 1. Por exemplo, 34 = 81.
Quando vemos escrito log3 9 , o que devemos
perguntar é: qual o expoente que eu devo elevar a base 3 para ter como
resultado da potência 9 ?
Neste
sentido, devemos multiplicar a base por ela mesma, e quantas vezes eu devo
multiplicar para obter o resultado da potência, e quantas vezes eu multiplico a
base para obter o resultado esse é o expoente, e logo esse será o logaritmo
buscado.
A
base 3 multiplicando por ela mesma (3 x 3 = 9) gera o nove, logo multipliquei 2
vezes o 3 por ele mesmo, o resultado será 2.
E aí teremos que log3 9 = 2.
Resolvendo log2 16, a pergunta será qual o expoente que devo elevar a base 2 para obter como resultado 16, multiplicamos o 2 por ele até obter o resultado 16, temos: 2 x 2 x 2 x 2 = 16, logo multipliquei 4 vezes o 2 por ele mesmo, o resultado será 4.
E aí teremos que log2 16 = 4.
Assim,
podemos descrever alguns exemplos:
a) log3 9 = 2, pois 32 = 9.
b)
log2 16 = 4, pois 24 = 16.
c)
log2 8 = 3, pois 23 = 8.
d)
log10 100 = 2, pois 102 = 100.
e)
log10 1.000 = 3, pois 103 = 1.000.
Sendo a e b números reais com a > 0, b > 0 e b ≠ 1, chama-se logaritmo de a na base b o expoente x tal que bx = a.
Na
sentença logb a = x,
‧ a é o
logaritmando
‧ b é a base do logaritmo
‧ x é o logaritmo de a na base b
Praticando:
Aplicando a definição de logaritmo, calcule:
a) log3 1 =
b) log3 3 =
c) log3 81 =
d) log3 34 =
e) log2 1 =
f) log2 2 =
g) log2 8 =
h) log2 64 =
i) log2 24 =
j) log5 53 =
Consequências da Definição:
a)
logb 1 = 0, para b > 0 e b ≠
1. (Logaritmo de 1 em qualquer base é zero)
b)
logb b = 1, para b > 0 e b ≠
1. (Logaritmo de um número igual a base é 1)
c) logb bN = N, para b > 0 e b ≠
1. (Logaritmo de uma potência com base igual à base do logaritmo é igual ao logaritmando)
Praticando:
Determine o valor da variável x, em cada item abaixo:
a) log3 x = 2
b) log3 x = 4
c) log2 x = 3
d) log2 x = 5
e) log3 3x = 13
Parte 2: Logaritmo Decimal
Antes da criação do logaritmo,
a simplificação das operações era uma tarefa árdua, pois eram resolvidas através
de relações matemáticas que exigiam esforços muito grandes que relacionavam
produtos com somas ou subtrações.
A mão do homem é a primeira calculadora de todos os tempos, porém o uso do corpo tem seus limites. A partir do século XVII, o logaritmo surgiu como um instrumento de cálculo para realizar simplificações das operações. Embora muitos matemáticos da época tenham trabalhado para chegar à forma atual do logaritmo, a invenção é creditada ao britânico John Napier (1550 – 1617).
John Nepier criou as tabelas logarítmicas com o objetivo de facilitar esses cálculos que exigiam bastantes esforços a princípio para seus trabalhos de Astronomia.
Por exemplo: 2 = 100,30103...
e 3 = 100,477121..., esse valores 0,30103... e 0,477121... são os
logaritmos de cada número correspondente na base 10.
Podemos escrever:
log10 2 = 0,30103... e log10 3 = 0,477121...
À esses valores de logaritmo, que são expoente de uma base 10 que geram os números do logaritmando são chamados de logaritmos decimais e por conveniência são apresentados sem o 10 na base do logaritmo.
Como log 2 = 0,30... e log 3 = 0,47...
Observação: Os logaritmos decimais que geralmente são apresentados de forma decimal, na realidade são números irracionais, que nos são apresentadas com suas devidas aproximações.
Vejam no link abaixo uma
tabela logarítmica mais detalhada:
https://www.somatematica.com.br/emedio/tablog10.php
Hoje, o logaritmo pode ser
utilizado nos mais variados campos de atuação, por exemplo, para o cálculo de
tempo de vida, usando o teste do carbono 14 e para estudar o crescimento de determinada
colônias de bactérias, na avaliação dos terremotos e muitos outros.
Normalmente, toda calculadora
científica possui a função que permite calcular o valor do logaritmo decimal ou
de base 10 de um número.
1) Na tabela logarítmica é nos dado que 2 = 100,301
e que 3 = 100,477:
6 = 2 x
3 = 100,301 x 100,477 = 100,778
b) Qual o logaritmo decimal de 6?
log 6 =
0,778
c) Calcule log 12.
Como 12
= 6 x 2 = 100,778 x 100,301 = 101,079.
Daí, log
12 = 1,079.
2) Consulte a tabela abaixo para responder as seguintes perguntas:
Significa que 100,6989 = 5.
b) Qual o valor de log 7 ?
log 7 = 0,8450
c) Qual o valor de 100,6020 ?
100,6020 = 4
d) Qual deve ser o expoente do número 10 para que o resultado a potência seja 8 ?
Como já visto, 8 = 4 x 2 = 100,6020 x 100.3010 = 100,9030.
Logo, o expoente deve ser 0,9030 ou pode-se dizer que log 8 =
0,9030.
Outra maneira de fazer é igualando 8 com 23 e utilizando a propriedade de potência de potência:
8 = 23 = (100.3010)3 = 100,9030.
E obtemos o mesmo resultado, como era esperado.
3) Aplicando a definição de logaritmo, calcule:
log 1 =
log 10 =
log 100 =
log 1000
log 0,1 =
log 0,01 =
log 10-5 =
Atividades:
1) Utilizando a definição achar o
valor de cada logaritmo abaixo:
a) log2 4
b) log2 16 c)
log2 32 d) log2 128
e) log2 ½
f) log2 1/4
g)log3 9 h) log3
27
i) log3 1/3 j)
log3 1/9 k) log3
34,21
2) Utilizando as consequências da definição, resolva os logaritmos abaixo:
a) log5 5 =
b) log9 9 =
c) logx x =
d) log7 1 =
e) log2 28 =
f) logx x-2 =
3) Um médico, após estudar o crescimento médio das crianças de uma
determinada cidade, com idades que variam de 1 a 12 anos, obteve a fórmula: h = 0,7 + log , em que h é a
altura (em metros) e i é a idade (em anos). Qual a altura, de um criança de 4
anos e uma de 9 anos?
4) (UERJ - 2016) Admita que a ordem de
grandeza de uma medida x é uma
potência de base 10, com expoente n inteiro, para 10n-1/2 ≤ x < 10n+1/2.
Considere que um terremoto tenha
liberado uma energia E, em joules,
cujo valor numérico é tal que log10 E = 15,3. A ordem de grandeza de E, em joules, equivale a:
(A) 1014. (B) 1015. (C) 1016. (D) 1017.
 |
A escala logarítmica não deslizante de Edmund
Gunter foi desenvolvida logo depois da invenção de Napier. O padre
inglês William Oughtred a aprimorou para criar a
régua de cálculo — um par de escalas logarítmicas móveis, em que os números são
colocados em distâncias proporcionais às diferenças de seus logaritmos.
Deslizando-se a escala superior em relação à escala inferior permite a soma
mecânica dos logaritmos. Por exemplo, colocando-se a distância de 1 a 2 na
escala inferior e a distância de 1 a 3 na escala superior, chega-se na escala
inferior ao produto 6. A régua de cálculo foi uma ferramenta essencial para
engenheiros e cientistas até a década de 1970, porque ela permite, em
detrimento da precisão, muito mais rapidez no cálculo que as técnicas baseadas
nas tabelas logarítmicas.
Parte 3: Propriedades do Logaritmo
Pela definição de logaritmo, temos que:
log 2 = 0,30 significa que 100,30 = 2;
log 3 = 0,48 significa que 100,48 =
3;
log 5 = 0,70
significa que 100,70 = 5 e
log 7 = 0,84
significa que 100,84 = 7.
Obtenha:
a) log 15
Fazemos 15 = 5 x 3 = 100,48 x 100,70 = 100,48 + 0,70 = 101,18 (utilizando o produto de potências de mesma base)
Logo, log 15 = 1,18.
d) log 25
Fazemos 25 = 52 = (100,70)2 =
100,70 x 2 = 101,40 (utilizando o potência de
potência)
Logo, log 25 = 1,40.
e) log 8
Logo, log 8 = 0,90.
Observe os logaritmos decimais de 2, 3, 6 e 8:
log 2 = 0,30; log 3 = 0,48; log 6 = 0,78; log 8 = 0,90.
Veja o que ocorre:
2º) log 6 – log 3 = log 2, isto é, log 6 – log 3 = log
6/3
3º) log 8 = 3 x log 2, isto é, log 23 = 3 x
log 2.
Daí, temos as propriedades dos
logaritmos:
1º) Produto: log a·b = log a + log b
“O
logaritmo de um produto é igual à soma dos logaritmos.”
2º) Quociente: log a/b = log a – log b
“O logaritmo de uma divisão é igual à subtração dos logaritmos.”
3º)
Potência: log ba =
a ·
log b
“O logaritmo de uma potência é igual ao produto do expoente dessa
potência com o logaritmo da base dessa potência.”
Exemplos:
a) Por isso, se temos log 2 = 0,30 e log 5 = 0,70 então log (2 x 5) = 0,30 + 0,70 = 1.
Logo, log 10 = 1.
b) Se temos log 8 = 0,90 e log 2 = 0,30 então log (8/2) = 0,90 – 0,30 = 0,60.
Logo, log 4 = 0,60.
c) Se temos log 2 = 0,30 então log 2–3 = (–3) x log 2 = (–3) x 0,30 = –0,90.
Logo, log 2–3 = –0,90.
Atividade: Aplicando as propriedades de logaritmo, calcule:
(Utilize log 2 = 0,30; log 3 = 0,48; log 5 = 0,70 e log 7 = 0,84)
a) log 4
Como 4 = 2 x 2 então log 4 = log (2 x 2) = log
2 + log 2 (propriedade de logaritmo de produto)
b) log 9
Como 9 = 3 x 3 então log 9 = log (3 x 3) = log 3 + log 3 (propriedade de logaritmo de produto)
c) log 15
Como 15 = 3 x 5 então log 15 = log (3 x 5) = log 3 + log 5 (propriedade de logaritmo de produto)
c) log 16
Como 16 = 4 x 4 então log 16 = log (4 x 4) = log 4 + log 4 (propriedade de logaritmo de produto)
Atenção: Em log 4, log 9 e log 16, poderíamos utilizar a propriedade
de logaritmo de potência:
log 4 = log 22 = 2 x log 2 = 2 x 0,30 = 0,60.
log 9 = log 32 = 2 x log 3 = 2 x 0,48 = 0,96.
log 16 = log 42 = 2 x log 4 = 2 x 0,60 = 1,20.
log 16 = log 24 = 4 x log 2 = 4 x 0,30 = 1,20.
d) log 20
Como 20 = 2 x 10 então log 20 = log (2 x 10) = log 2 + log 10 (propriedade de logaritmo de produto)
e) log 21
Como 21 = 3 x 7 então log 21 = log (3 x 7) = log 3 + log 7 (propriedade de logaritmo de produto)
f) log 32
Como 32 = 25 então log 32 = log 25
= 5 x log 2 (propriedade de logaritmo de potência)
g) log 54
Utilizando a propriedade de logaritmo de potência, temos:
log 54 = 4 x log 5 = 4 x 0,70 = 2,80.
h) log 64
Como 64 = 26 então log 64= log 26 = 6 x log 2 (propriedade de logaritmo de potência)
i) log
21 / 5
Utilizando a propriedade de logaritmo de divisão, temos:
log 21 / 5 = log 21 – log 5 = 1,32 x 0,70 = 0,62.
Atividades
1) Aplicando a definição, calcule os logaritmos:
a) log5 25
b) log5 125
c) log7 7
d) log7 49
e) log7 343
f) log5 1
g) log5 1/5
h) log5 1/25
i) log7 1/7
j) log7 1/49
2) Dados log 5
= 0,70 e log 7 = 0,84. Calcule:
a) log 35 b) log 7/5 c) log 5/7 d) log 49
e) log 25 f)
log 125 g) log 50 h) log 70
i) log 100/7 j) log 0,7 k) log 0,05 l) log 0,35
1) Aplicando a definição, calcule os logaritmos:
a) log8 64
b) log4 64
c) log6 36
d) log4 4
e) log9 9
f) log6 1/36
g) log4 1/16
h) log 10.000
i) log 0,0001
j) log 10-6
k) log9 1
2) Utilizando log 2 = 0,30, log 7 = 0,84, calcule:
a) log 14
b) log 7/2
c) log 2/7
d) log 40
e) log 0,14
f) log 210
3) Utilizando as propriedades
dos logaritmos, determine o valor de cada expressão:
A = log 2 + log 5
B = log8 2 + log8 32
C = log6 3 + log6 12
D = log 2 + log 20 + log 25
E = log15 60 – log15 4
F = log2 96 – log2 3
G = log2 96 – log3 3
H = log4 6 + log4 32 – log4 3
I = log2 21 – log2 28 – log2 6
J = log6 18 + log6 30 – log6 3 – log6 5
Parte 4 - Logaritmo com Equações
O logaritmo pode ser utilizado como ferramenta de resolução de equações em que aparece exponenciais de bases distintas ou quando aparece os próprios logaritmos na equação. Atenção, que esses tipos de equações terão como base de resolução a definição e as propriedades de logaritmo estudados anteriormente.
Exemplos:
1) Encontre o valor de x em cada uma
das equações:
a) log x = log 4
Numa
igualdade de logaritmos, se as bases são iguais então os logaritmandos são
iguais.
Como temos base 10 nos dois lados, logo x = 4.
b) log8 (x + 3) = log8
(3x − 7)
Nesse caso, temos o mesmo do anterior, igualdade de logaritmos com bases iguais, então:
log8 (3x − 7) = log8 (x +
3) ⇒ 3x − 7 = x + 3 ⇒
2x = 10 ⇒ x = 5.
c) log x = log 3 + log 5
Como, tem-se soma de dois logaritmos de um dos
lados, então, utilizando a propriedade de produto de logaritmo, a soma de dois
logaritmos se torna logaritmo do produto dos dois logaritmandos, daí:
log x = log 3 + log 5 ⇒
log x = log (3 x 5) ⇒
log x = log 15 ⇒
x = 15.
d) log 2 + log (x – 3) = 1
Como no anterior, tem-se soma de dois logaritmos de um dos lados, então, utilizando a propriedade de produto de logaritmo, a soma de dois logaritmos se torna logaritmo do produto dos dois logaritmandos, porém no outro membro tem-se 1 e o 1 é resultado do logaritmo do mesmo número da base, então 1 = log 10, daí:
log 2∙(x − 3) = log 10 ⇒ log (2x − 6) = log 10 ⇒ 2x − 6 = 10 ⇒ 2x = 16 ⇒ x = 8.
e) log (5x – 12) – log x = 0
Utilizando a propriedade de logaritmo de
divisão de logaritmo no primeiro membro e no segundo membro tem-se 0 que é o
resultado de logaritmo de 1 em qualquer base, daí:
2) Utilizando log 3,17 = 0,5, calcule
o valor de x, tal que:
a) (3,17)x = 100
Para resolver uma equação exponencial com bases
diferentes, devemos utilizar a seguinte ideia: numa igualdade de duas
expressões, serão iguais os logaritmos das duas expressões.
Dessa forma, tem-se:
Se (3,17)x = 100, então log (3,17)x =
log 100.
Da equação logarítmica surgida, utilizamos a
propriedade de logaritmo de potência, daí:
b) (3,17)x = 0,01
Como
acima:
3) Dado log 3 = 0,48 e log 5 = 0,70, calcule o valor de x na equação: 10x = 15.
log 10x = log 15
x ∙
log 10 =
log 3 + log 5
x ∙
1 = 0,48 + 0,70
x = 1,18
Atividades:
1) Utilizando a definição de
logaritmo, calcule o valor de x nas
equações abaixo:
a) log3
x = 4
b) log5
x = 3
c) log2
8 = 2x
d) log5
(x+1) = 0
e) log2 4x = 5
f) log5 (x+1) = 0
g) log8 (3 – 2x) = 0
h) logx (2x – 7) = 1
i) log2 8 = 3x
j) log3 9 = 2x
2) Utilizando as propriedades dos logaritmos, determine o valor de x cada equação:
a) log x = log 56
b) log x = log 6 + log 7
c)log x = log 54 – log 9
d) log (x+6) + log 3 = log 6
e) log (5x + 10) – log x = 1
f) log (x + 3) + log 2 = 2
g) log (x – 2) – 3·log 1 = 1
h) log 2x – 2·log 2 = log (x – 2)
3) Utilizando as propriedades dos logaritmos, determine o
valor de cada expressão:
A
= log5 15 + log5 10 – log5 6
B=
log 30 + log 7 – log 21
C
= log2 100 – log2 25
D
= log3 15 – log3 5
E
= log7 28 – log7 4
F = 2 · log4 8
G = log5 10 + log5 2
– 2![]() log5 2
log5 2
Outras:
1) Utilizando as propriedades dos
logaritmos, determine o valor de cada expressão:
A = log4 8 + log4 8
B = log 4 + log 25
C = log15 9 + log15 25
D = log2 48 + log2 1/3
E = log5 500 + log5 2 + log5
1/8
F = log7 98 – log7 2
G = log4 192 – log4 3
H = log5 20 + log5 3 – log5
12
I = log5 6 – log5 15 – log5
10
J = log2 36 + log2 3 – log2
6 – log2 9
Veja aqui Aplicações de Logaritmo
Aprofunde-se:











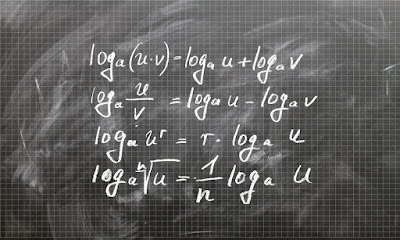



Nenhum comentário:
Postar um comentário