As medidas resumo (de posição
e de dispersão) correspondem a uma síntese do conjunto de dados observados e ao
passo preliminar para fazer uma inferência
estatística, ou seja, a partir das informações obtidas na amostra, expandir
nossas conclusões para a população. Como as distribuições podem apresentar
formas variadas é importante conhecer diferentes tipos de medidas resumo, tanto
de posição como de dispersão, para usar medidas apropriadas em cada.
Vejamos agora as medidas de Posição ou de Tendência Central.
Medidas de Posição, como o
próprio termo indica, visam a resumir um conjunto de dados em geral numa única
medida em algum lugar geométrico entre os extremos observados do conjunto
(mínimo e máximo).
Veja na figura, as marcações
da média e da mediana das notas de Artes sem bonificação, observe que foram posicionadas
no centro dos dados da observação por isso chama-se também de medidas de
tendência central.
Só é possível obter medidas
como a média e a mediana, se nossas observações são de natureza quantitativa, pois, as variáveis qualitativas estão no
domínio da frequência apenas, ou
seja, só podemos contar quantas observações ocorrem em cada categoria da
variável qualitativa, mas não podemos operar matematicamente com as categorias
em si.
Por exemplo, na atividade
Prática de Atividades Físicas, trabalhamos com a variável
modalidade do esporte praticado. As modalidades correspondem à “Futebol”,
“Caminhada”, “Fitness”, etc. Observe que são respostas não numéricas e, por
isso, não podemos calcular uma média e não existe uma relação de ordem natural
das respostas. Apenas podemos ordenar as
respostas pela frequência na qual elas ocorreram.
As principais medidas de posição usadas na Estatística são a média, a mediana, a moda e os quartis da distribuição. Outras medidas de posição existem, mas não são tão usuais.
Definiremos a seguir as
principais medidas que buscam de alguma forma resumir a informação dos dados coletados.
1) A média aritmética de vários números representa a soma de todos esses
números dividida por quantos forem esses números. Cinco alunos de uma escola
foram premiados pela pontuação obtida numa competição. As idades, em anos, são:
1º lugar: Simão – 17 anos
2º lugar: Edite – 15 anos
3º lugar: Teresa – 16 anos
4º lugar: Tito – 15 anos
5º lugar: Nuno – 17 anos
Com base nos dados acima, qual é a idade média dos alunos premiados nessa escola?
Nesse caso, procedemos com a soma de todas as idades: 17 + 15 + 16 + 15 + 17 = 80 e divide o resultado obtido da soma pelo número das colocações:
80 / 5 = 16.
Logo, a média das idades dos premiados é 16 anos.
2) A moda é o elemento ou os elementos de um
conjunto que aparece/aparecem com mais frequência.
Em uma
determinada pesquisa feita sobre as idades dos alunos de uma turma da Escola A,
obtivemos os resultados abaixo:
Logo, a moda dessa frequência é 17 anos.
3) A mediana é o valor central de uma
amostra apresentada.
a) Rebeca tem 5 filhos, com as seguintes idades: 3 anos, 6 anos, 9 anos, 12 anos e 15 anos. Qual a mediana das idades de seus filhos?
Se o conjunto de dados tem uma quantidade ímpar
de elementos então, considerando os dados ordenados, a mediana ocupará a
posição central.
Por exemplo, no caso do problema se o conjunto de dados tem 5 elementos, a posição central será a terceira posição. Nesse caso, haverá, ordenadamente, dois elementos anteriores e dois posteriores à mediana.
Ordenando as idades, temos: 3, 6, 9, 12, 15.
A mediana da amostra é 9 anos.
b) Rute tem 4 filhos cujas idades são 3, 6, 8 e 15 anos. Qual a mediana das idades de seus filhos?
Se o
conjunto de dados tem uma quantidade par de elementos não será possível
identificar “um” elemento central. Nesse caso, para a determinação da mediana
serão considerados os dois elementos centrais da sequência ordenada. A mediana
é dada pela média aritmética desses elementos. Por exemplo, nesse caso, o
conjunto de dados tem 4 elementos, então as posições centrais são a 2ª e a 3ª.
A mediana será a média dos elementos que ocupam essas posições na sequência ordenada.
Ordenando as idades, temos: 3, 6, 8, 15.
Procedemos
com a média entre 6 e 8:
(6 + 8)
/ 2 = 14 / 2 = 7.
Logo,
a mediana das idades é 7 anos.
4) Ester, para viajar num feriadão, decidiu fazer algumas economias. Ela poupou durante seis meses os seguintes valores apresentados na tabela abaixo.
Com base nas informações acima, qual foi a média mensal das economias de Ester?
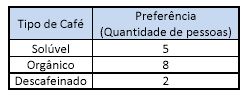
5) Uma
pesquisa sobre a preferência de café foi feita com 15 pessoas de um determinado
município. Observe a tabela abaixo, e responda qual é a moda dessa
distribuição.
6) A
tabela abaixo apresenta dados referentes ao consumo de energia elétrica de uma residência,
em quilowatt-hora, no período de outubro a dezembro.
Com base nas informações acima, determine o consumo mediano de energia elétrica nos períodos citados.
7) Raquel
nos últimos 7 dias gastou, em reais, as seguintes quantias:
Determine o gasto mediano que Raquel teve nesses dias.
8) A
tabela abaixo mostra a distribuição das notas em Matemática obtidas pelos 12 alunos
de uma turma, durante o período de avaliação:
a)
Determine a moda dessa distribuição de notas.
b)
Determine a mediana dessa distribuição de notas.
9) Suponha que na primeira segunda-feira do mês de março de 2018, um Posto de Saúde tenha registrado as idades (em anos completos) das seis primeiras pessoas que chegaram para tomar a vacina da febre amarela e, os registros, obtidos foram {55, 22, 30, 14, 25, 40}.
a) Qual a média de idade dessa
amostra?
b) Qual a mediana das idades?
c) É possível calcular a moda
dessa amostra?
10) As idades, em anos, de um grupo de sete pessoas são: 16, 8, 13, 8, 10, 8, 21. A respeito dos dados, podemos dizer:
11) Uma escola utiliza um método de avaliação muito diferente dos tradicionais. O método consiste em:
I – Os alunos são submetidos a seis provas regulares de cada
matéria ao longo do ano.
II – O aluno é considerado aprovado se a mediana das
notas das nove provas for maior ou igual a sete, caso contrário reprovado.
Em Matemática, as seis notas do aluno Benedito foram 7, 8, 3, 5, 9, 5. Sabendo-se disso, então:
(A) Benedito foi
reprovado, pois sua mediana foi igual a 5.
(B) Benedito foi reprovado, pois sua
mediana foi igual a 6.
(C) Benedito foi aprovado, pois sua
mediana foi igual a 7.
(D) Benedito foi aprovado, pois sua
mediana foi igual a 8.
12) Uma pessoa está disputando um processo de seleção para uma vaga de emprego em um escritório. Em uma das etapas desse processo, ela tem de digitar oito textos. A quantidade de erros dessa pessoa, em cada um dos textos digitados, é dada na tabela.
Nessa etapa do processo de seleção, os candidatos serão avaliados pelo valor da mediana do número de erros. A mediana dos números de erros cometidos por essa pessoa é igual a:
(A) 2,0 (B) 2,5 (C) 3,0 (D) 3,5
13) Ao final de um trimestre, um professor de Artes registrou as seguintes notas de seus 35 alunos, listadas no quadro a seguir, em ordem crescente. E a seguir construiu um histograma de distribuição de frequência das notas disposta ao lado como na figura abaixo:
b) Qual a moda das notas da
turma?
c) Qual a média das notas da
turma?
14) Sara fez treˆs provas de Matema´tica no primeiro bimestre. Suas notas foram 7, 8 e 9. Determine sua me´dia em Matema´tica neste bimestre. Qual a mediana e a moda dessas notas?
15) Um dado foi lanc¸ado 15 vezes e os resultados obtidos esta˜o representados na tabela abaixo:
|
Nu´ mero |
Frequeˆncia |
|
1 |
3 |
|
2 |
4 |
|
3 |
0 |
|
4 |
2 |
|
5 |
3 |
|
6 |
3 |
Determine:
a) moda.
b) mediana.
16) Um atleta,
em treinamento para as olimp´ıadas, corre quatro vezes por semana, sendo
que nas segundas- feiras, ele percorre
5km; nas terc¸as, 7km; nas quintas
8km; e, por
fim, nos
sa´bados, 8km. Determine:
a) distaˆncia me´dia por dia de treino que esse atleta percorre.
b) distaˆncia me´dia por dia da semana que esse atleta percorre.
c) distaˆncia percorrida
para que
sua me´dia por
dia da semana seja 6km, se ele decide correr também aos domingos.
17) A tabela abaixo
mostra o faturamento de uma empresa no primeiro semestre de 2016.
|
|
Meˆs |
Faturamento (R$) |
|
jan |
4.000 |
|
|
fev |
12.000 |
|
|
mar |
8.500 |
|
|
abr |
7.500 |
|
|
maio |
10.000 |
|
|
jun |
12.000 |
|
|
|
|
|
a) média mensal de faturamento.
b) o faturamento total do segundo semestre, para que o faturamento
médio mensal no ano de 2016 seja R$10.000,00.
18) Em uma escola com 200 alunos, as idades são distribuídas de acordo com a tabela abaixo:
Determine:
a)
a moda.
b)
a mediana.
c)
a média.
19) Deseja-se
comprar lentes para óculos. As lentes devem ter espessuras mais próximas possíveis
da medida 3mm. No estoque
de uma loja, há lentes de espessuras: 3,10mm;
3,021mm; 2,96mm; 2,099mm e 3,07mm. Determine a espessura média dessas
medidas.
20) Um aluno
compara as notas das 6 provas de Português que fez em 2004 e de outras 6, da mesma
matéria, que fez em 2005. Ele repara que em 5 provas ele obteve as mesmas notas
nos dois anos. Na outra prova a nota foi 86 em 2004 e 68 em 2005. Em 2004 a média
aritmética das seis notas foi 84. Qual foi a média em 2005?
(A) 78.
(B) 81.
(C) 82.
(D) 83.
(E) 87.
21)
Rubens foi fazer na calculadora a média de suas quatro notas
de Matemática.
O resultado obtido foi 8, mas ele
percebeu que havia digitado uma nota errada, trocando 5 por 7. Qual o valor correto
para a média?
22) Em um concurso,
são aprovados para a segunda fase todos que acertam uma quantidade
maior de questões que o número mediano de questões acertadas por todos os candidatos.
Observe o resultado da primeira fase na tabela, que mostra a quantidade de candidatos
por número de acertos.
23) Em uma seletiva para a final dos 100 metros livres de natação, numa olimpíada, os atletas, em suas respectivas raias, obtiveram os tempos conforme a tabela. A mediana dos tempos apresentados na tabela é:
|
|
Raia |
Tempo
(segundo) |
|
1 |
20,90 |
|
|
2 |
20,90 |
|
|
3 |
20,50 |
|
|
4 |
20,80 |
|
|
5 |
20,60 |
|
|
6 |
20,60 |
|
|
7 |
20,90 |
|
|
8 |
20,96 |
|
|
|
|
|
(A) 20, 70.
(B) 20, 77.
(C) 20, 80.
(D) 20, 85.
(E) 20, 90.
Parte 2 - Distribuição de Frequência
Observe cada uma das variáveis
a seguir e indique se cada uma delas é uma variável qualitativa ou quantitativa.
Se for uma variável qualitativa,
indique se ela é binária (apenas duas respostas possíveis) ou não.
a) altura (em metros)
b) peso (em quilos)
c) razão do peso sobre o quadrado
da medida da altura
d) tempo de sono na noite
anterior
e) se foi dormir na noite
anterior antes ou depois da meia-noite
f) mês de nascimento
g) número de irmãos
h) nota obtida na última
avaliação de Matemática
i) se tirou nota maior ou
igual a 6,0 ou menor do que 6,0 na última avaliação de Matemática
j) distância da casa à escola
k) se o indivíduo possui
cartão de crédito ou não
l) modo de locomoção para a
escola
Em análise dados estatísticos, se a variável for quantitativa e ordinal dispomos as respostas em ordem crescente.
Se a variável é nominal,
podemos dispor as respostas em ordem decrescente de frequência.
EXEMPLO
Numa turma de um colégio foram
observados os tipos sanguíneos de seus 40 alunos.
Verificou-se que 18 alunos têm
sangue tipo “O”, 12, tipo “A”, 6, tipo “AB” e 4, tipo “B”.
Nesse exemplo, temos que as frequências absolutas para os tipos sanguíneos “O”, “A”, “AB” e “B” foram, respectivamente, 18, 12, 6 e 4.
Em geral, quando queremos
comparar grupos diferentes, usamos a frequência
relativa em vez da frequência
absoluta.
A frequência relativa é dada pela razão entre a frequência absoluta e o número total de observações. Nesse exemplo, temos que as frequências relativas para os tipos sanguíneos “O”, “A”, “AB” e “B” foram, respectivamente, 0,45; 0,30; 0,15 e 0,10. Observe que em termos percentuais as frequências relativas observadas equivalem a, respectivamente, 45%, 30%, 15% e 10%.
É comum resumir esse tipo de
informação, usando uma tabela, informando as respostas da variável e suas frequências.
Nesse exemplo a variável é tipo sanguíneo e sua classificação é qualitativa nominal,
pois assume respostas não numéricas “A”, “B”, “AB” e “O”, sem uma ordenação natural.
Em geral dispomos os valores dessa variável em ordem decrescente de frequência.
As representações gráficas
mais comuns são gráficos de barras e gráficos de setores. Para comparações
da mesma variável em grupos diferentes é comum usar o gráfico de barras
múltiplas com frequências relativas ou porcentagens.
Os gráficos de barras são úteis para descrever a distribuição de frequências de uma variável qualitativa. Nesse gráfico só há um eixo com escala que corresponde aos valores das frequências das categorias (respostas) da variável.
As barras podem ser tanto verticais como
horizontais e são apresentadas de forma igualmente espaçada. Cada barra
representa uma resposta da variável qualitativa e a altura da barra corresponde
à frequência daquela resposta. Observe que o posicionamento das barras é livre,
conforme as figuras a seguir.
O mais comum é dispor as respostas em ordem decrescente de frequência. Esse tipo de gráfico também pode ser usado para representar uma variável quantitativa discreta, sendo que nesse caso, as posições das barras correspondem aos valores assumidos pela variável, como é mostrado no gráfico acima.
Pela natureza discreta da variável, as barras não são adjacentes e, pela natureza quantitativa da variável, o posicionamento das barras não é livre.
Já o gráfico em setores é muito utilizado para apresentação de frequências relativas à amostra analisada, como no seguinte:
Média, Mediana e Moda de Distribuição de frequência
Na amostra dos tipos sanguíneos, como os dados já foram agrupados em distribuição de suas frequências, é preciso observar que qualquer que seja o estudo, é necessária a descrição de todas as variáveis envolvidas. Para as variáveis qualitativas, como grupos sanguíneos, é apenas possível apresentar o número e a percentagem. Já para as variáveis quantitativas, como idades e alturas, apresentam-se a média, moda, mediana, quartis, desvio padrão, de acordo com as necessidades.
Observem o time de futebol apresentado abaixo com os 11 componentes de um time e suas respectivas alturas.
Como a altura é variável é quantitativa, podemos fazer a distribuição de frequência das alturas e notas suas medidas conforme a necessidade.
Nesse caso, a média será a soma da
quantidade de vezes que cada termo aparece cada frequência absoluta, dividida
pela quantidade de observações realizadas, no casa quantas alturas foram
notadas.
Assim, temos que a média das alturas ou a altura média do time é dada por:
Daí, a média da altura do
time é 1,62 metros.
A média é considerada “ponderada” quando os valores dos conjuntos tiverem pesos ou frequências diferentes, como nesse caso.
Na
tabela de distribuição, as alturas foram colocadas em ordem crescente, como
temos 11 dados de observações, a mediana da distribuição estará na 6ª posição.
Observando a tabela, verifica-se que o dado que está na 6ª posição é 1,64.
Logo,
a mediana da distribuição é 1,64 metros.
Dados
agrupados por valores discretos, a moda
é o valor com maior frequência. Como
observado na tabela de distribuição, o valor com maior frequência é 1,66.
Logo,
a moda da distribuição é 1,66 metros.
Em qualquer dos casos podem apresentar-se os valores para a totalidade da
amostra ou por grupos.
Atividades:
1) Num curso de Inglês, a distribuição das idades dos alunos é dada pelo gráfico seguinte.
Com base nos dados do gráfico, determine:
a) o
número total de alunos do curso.
b) o
número de alunos com no mínimo 19 anos.
c) A
média, a mediana e a moda das idades dos alunos.
d) escolhido
um aluno ao acaso, qual a probabilidade de sua idade exatamente 16 anos.
2) Para
analisar o rendimento de uma turma, um professor registrou as notas dos seus 20
alunos, a saber:
0 9
10 5 5
8 3 4 10
7
3 8
2 6 9
2 8 10
1 2
3) As áreas construídas, medidas em metros quadrados, de vinte residências
de certa região são:
250 280 330 400 380
300 250 280 330 300
400 380 280 280 400
380 300 280 250 250
Construa uma tabela de distribuição de frequência
dessa amostra com os dados das áreas e o número de casas com cada áreas e
determine a média, a mediana e moda da frequência.
4) Preocupada com seus resultados, uma empresa fez um balanço dos lucros obtidos nos últimos sete meses, apresentado na tabela abaixo:
a)
Determine a média, a moda e a mediana dos lucros nos sete meses.
b) Avaliando
os resultados, o conselho diretor da empresa decidiu comprar, nos dois meses subsequentes,
a mesma quantidade de matéria-prima comprada no mês em que o lucro mais se
aproximou da média dos lucros mensais dessa empresa nesse período de sete meses.
Nos próximos dois meses, de qual mês anterior essa empresa deverá comprar a mesma
quantidade de matéria prima?
5) Em uma seletiva para a final dos 100 metros livres de natação, numa olimpíada, os atletas, em suas respectivas raias, obtiveram os seguintes tempos:
(A) 20,70. (B) 20,77. (C) 20,80. (D) 20,85.
6) Observe no gráfico a seguir uma representação para as notas de 50 alunos do 3º ano do Colégio Sucesso na disciplina de Matemática.
Determine a média, a mediana e a moda
das notas desses alunos.
7) O quadro
abaixo mostra o consumo de gasolina do carro de Silas, em três viagens.
Considerando-se as três viagens, qual foi o consumo médio de gasolina do carro de Silas?
(A) 6,6
km/litro
(B) 7,0
km/litro
(C) 7,3
km/litro
(D) 8,0
km/litro
8) No curso de inglês de Celina, os quatro bimestres valem 100 pontos cada, e a nota final é calculada fazendo-se a média aritmética entre as quatro notas bimestrais. Um aluno é considerado aprovado se sua média final for maior ou igual a 60.
As
notas de Celina, nos três primeiros bimestres, foram:
•
1º bimestre: 50.
•
2º bimestre: 60.
•
3º bimestre: 67.
Qual
a nota mínima que Ana deverá obter no 4º bimestre para que seja aprovada?
(A)
60. (B) 61. (C) 63. (D) 67.
9) Abaixo,
estão as três primeiras notas de Estanislau num curso de idiomas:
6,3 + 7,0 + 5,3.
Para ser aprovado, a média das notas das quatro provas obrigatórias deve ser maior ou igual a 7,0. Caso contrário, o aluno fica em recuperação. Qual a menor nota que Estanislau deve tirar para não ficar em recuperação?
(A)
7,0 (B) 7,9 (C) 8,3
(D) 9,4
10) A média aritmética de um conjunto de cinco valores é igual a 12,4. Retirando-se o número 10 desse conjunto, qual será a nova média?
(A) 10,0. (B) 10,4. (C) 12,0. (D) 13,0.
11) A
média de idade dos 20 professores de uma escola era 40 anos. O professor mais
velho, que tinha 60 anos, aposentou-se e, em seu lugar, foi contratado um
professor de 40 anos de idade. Com essa alteração, a média de idade dos
professores dessa escola passou a ser:
(A)
40 anos. (B) 39 anos. (C) 30 anos.
(D) 20 anos.
12) Em 2019, o salário de Simão foi de R$ 1.000,00 por mês durante os 6 primeiros meses do ano, R$ 1.200,00 por mês nos 5 meses seguintes, e R$ 1.500,00, em dezembro. Em 2019, o salário médio mensal de Simão foi:
(A) R$ 1.200,00
(B) R$ 1.125,00.
(C) R$ 1.000,00.
(D) R$ 1.450,00.
13) Uma pesquisa feita com 100 empregados de uma empresa metalúrgica mostrou os seguintes resultados:
O salário
médio dos 100 empregados dessa empresa é:
(A) R$ 1.000,00.
(B) R$ 1.160,00.
(C) R$ 1.300,00.
(D) R$ 1.333,33.
Qual
é a média de gols desse time no campeonato?
(A)
1,5. (B) 2,2. (C) 2,7.
(D) 5,5.
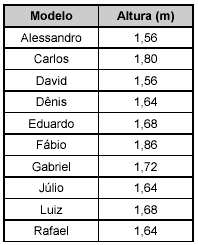
Qual é a
moda e a mediana, em metros, das alturas desses modelos, respectivamente?
(A) 1,64 e 1,66. (B) 1,64 e 1,77.
(C) 1,86 e 1,77. (D) 1,86 e 1,66.
16) Isabel pediu a todas as pessoas convidadas para a sua festa de aniversário que levassem, uma playlist de suas músicas favoritas. Ela perguntou a todos os convidados quantas playlists cada um deles iria levar e fez uma lista onde escreveu todas as respostas. Depois que ela ordenou todas as respostas, em ordem crescente, as primeiras 15 respostas foram:
1, 1, 1,
1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 4, 5.
Sabendo
que a mediana de todas as respostas dadas é igual a 4 e que a quantidade de
pessoas que foram à festa é ímpar, quantas pessoas foram convidadas para a
festa de aniversário de Isabel?
(A) 13 (B)
26 (C) 27 (D) 34
(A) A metade dos alunos leu exatamente dois livros.
(B) Essa turma leu exatamente 45 livros.
(C) A média da quantidade dos livros lidos foi de 2,25 livros.
(D) O total de alunos desta turma é 24 alunos.
18) (ENEM-2017) Três alunos, X, Y e Z, estão matriculados em um curso de inglês. Para avaliar esses alunos, o professor optou por fazer cinco provas. Para que seja aprovado nesse curso, o aluno deverá ter a média aritmética das notas das cinco provas maior ou igual a 6. Na tabela, estão dispostas as notas que cada aluno tirou em cada prova.
Com base nos dados da tabela e nas informações dadas, ficará(ão) reprovado(s):
(A) apenas o aluno Y.
(B) apenas o aluno Z.
(C) apenas os alunos X e Y.
(D) apenas os alunos X e Z.
(E) os alunos X, Y e Z.
19) (ENEM-2019) Em uma fábrica de refrigerantes, é necessário que se faça periodicamente o controle no processo de engarrafamento para evitar que sejam envasadas garrafas fora da especificação do volume escrito no rótulo.
Diariamente, durante 60 dias, foram anotadas as quantidades de garrafas fora dessas especificações. O resultado está apresentado no quadro.
(A)
0,1
(B) 0,2
(C) 1,5
(D) 2,0
(E) 3,0
20) (ENEM-2016) Um posto de saúde registrou a quantidade de vacinas aplicadas contra febre amarela nos últimos cinco meses:
1º mês: 21;
2º mês: 22;
3º mês: 25;
4º mês: 31;
5º mês: 21.
No início do primeiro mês, esse posto de saúde tinha 228 vacinas contra febre amarela em estoque. A política de reposição do estoque prevê a aquisição de novas vacinas, no início do sexto mês, de tal forma que a quantidade inicial em estoque para os próximos meses seja igual a 12 vezes a média das quantidades mensais dessas vacinas aplicadas nos últimos cinco meses. Para atender essas condições, a quantidade de vacinas contra febre amarela que o posto de saúde deve adquirir no início do sexto mês é:
(A) 156. (B) 180. (C) 192. (D)
264.
21) (ENEM-2017) O gráfico apresenta a taxa de desemprego (em %) para o período de março
de 2008 a abril de 2009, obtida com base nos dados observados nas regiões
metropolitanas de Recife, Salvador, Belo Horizonte, Rio de Janeiro, São Paulo e
Porto Alegre.
22) (ENEM-2010) O quadro seguinte mostra o desempenho de um time de futebol no último campeonato. A coluna da esquerda mostra o número de gols marcados e a coluna da direita informa em quantos jogos o time marcou aquele número de gols.
Se
X, Y e Z são, respectivamente, a média, a mediana e a moda desta
distribuição, então:
(A) X = Y < Z.
(B) Z < X = Y
(C) Y < Z < X.
(D) Z < X < Y
(E) Z < Y < X








































Nenhum comentário:
Postar um comentário