Operações com Polinômios (Soma, Subtração e Multiplicação)
Já foram apresentadas funções polinomiais. Nesta aula, será aprofundado um pouco mais o seu conhecimento no estudo dessas funções, aprendendo a efetuar cálculos de adição, subtração e multiplicação.
As situações envolvendo cálculos algébricos são de extrema importância para a aplicação de regras nas operações entre os monômios. As situações aqui apresentadas abordarão a adição, a subtração e a multiplicação de polinômios.
1 – ADIÇÃO DE POLINÔMIOS:
A adição entre polinômios é realizada de forma muito simples, basta reduzir seus termos semelhantes, vejamos alguns exemplos a seguir.
Dados dois polinômios A(x) = 3x2 – 6x + 4 e B(x) = 2x2 + 4x – 7.
A soma A(x) + B(x) é calculada da seguinte forma:
A(x) + B(x) = (3x2 – 6x + 4) + (2x2 + 4x – 7)
1º passo: Eliminando os parênteses e observando os sinais das operações, temos:
A(x) + B(x) = 3x2 – 6x + 4 + 2x2 + 4x – 7
2º passo: Reduzindo os termos semelhantes.
A(x) + B(x) = 3x2 + 2x2 – 6x + 4x + 4 – 7
A(x) + B(x) = 5x2 – 2x – 3
Viu como é simples!!
Agora vamos trabalhar alguns exemplos onde é preciso ter bastante atenção!
EXEMPLO 01:
Considere as funções polinomiais A(x) = determine a soma A(x) + B(x).
Resolução:
Para determinar a soma A(x) + B(x) utilizaremos os passos apresentados acima:
A(x) + B(x) = (x3 + 2x2 +x – 3) + (x2 + x + 1)
A(x) + B(x) = x3 + 2x2 + x – 3 + x2 + x + 1
A(x) + B(x) = x3 + 2x2 + x2 + x + x – 3 + 1
A(x) + B(x) =
EXEMPLO 02:
Considere os polinômios P(x) = –2x² + 5x – 2 e Q(x) = –3x³ + 2x – 1. Vamos efetuar a adição entre eles.
Resolução:
P(x) + Q(x) = (– 2x² + 5x – 2) + (–3x³ + 2x – 1)
P(x) + Q(x) = –2x² + 5x – 2 – 3x³ + 2x – 1
P(x) + Q(x) = –3x³ – 2x² + 7x –
3
2 - SUBTRAÇÃO DE POLINÔMIOS:
A subtração entre polinômios é realizada de forma análoga a adição, basta que ao eliminar os parênteses você se lembre de que o sinal de subtração altera o sinal de todos os termos dentro do parênteses.
Dados dois polinômios A(x) = 3x2 – 6x + 4 e B(x) = 2x2 + 4x – 7.
A diferença A(x) – B(x) é calculada da seguinte forma:
A(x) – B(x) = (3x2 – 6x + 4) – (2x2 + 4x – 7)
1º passo: Elimine os parênteses observando que os sinais dos termos do polinômio B(x) devem ser trocados. Observe:
A(x) – B(x) = (3x2 – 6x + 4) – (2x2 + 4x – 7)
A(x) – B(x) = 3x2 – 6x + 4 – 2x2
– 4x + 7
2º passo: Reduzindo os termos semelhantes.
A(x) – B(x) = x2 – 10x + 11
Viu como subtrair polinômios também é simples!!
Agora veja alguns exemplos onde também é preciso ter bastante atenção!
EXEMPLO 03:
Considere as funções
polinomiais A(x) = x3 + 2x2 + x – 3 e
B(x) = x2 + x + 1, determine a diferença A(x) – B(x):
Resolução:
A(x) – B(x) = (x3 + 2x2 + x – 3) – (x2 + x + 1), seguindo os passos anteriores:
1º passo: Eliminando
os parênteses e observando os sinais das operações, temos:
A(x) – B(x) = x3 + 2x2 + x – 3 – x2 – x – 1
2º passo: Reduzindo
os termos semelhantes.
A(x) – B(x) = x3 + x2
– 4
EXEMPLO 04:
Considere os polinômios P(x) = –2x² + 5x– 2 e Q(x) = – 3x³ + 2x – 1. Vamos efetuar a subtração
entre eles.
Resolução:
P(x) – Q(x) = (–2x² + 5x - 2)
– (–3x³ + 2x – 1)
P(x) – Q(x) = – 2x² + 5x –
2 + 3x³ – 2x + 1
P(x) – Q(x) = 3x³ – 2x² + 3x – 1
3 - MULTIPLICAÇÃO DE UM MONÔMIO POR UM POLINÔMIO:
Para desenvolver o produto de um monômio por um polinômio é primordial o conhecimento sobre a propriedade distributiva da multiplicação, pois esta multiplicação é feita multiplicando-se o monômio por cada termo do polinômio. Vejam alguns exemplos:
EXEMPLO 05:
Considere o monômio A(x) = 2x e o polinômio B(x) = x2 + x + 1, determine a
multiplicação A(x) ∙ B(x):
Resolução:
A(x)∙B(x) = 2x∙(x2
+ x + 1), utilizando a propriedade distributiva da multiplicação, isto é, deveremos
multiplicar o monômio A(x) por cada
termo do polinômio B(x).
A(x)∙B(x) = 2x∙(x2 + x + 1)
= 2x3 + 2x2 + 2x
EXEMPLO 06:
Dados o monômio P(x) = 2x2 e o polinômio Q(x)
= 3x3 + 2x2 + x + 1,
determine o produto P(x) ∙ Q(x).
Resolução:
O produto P(x)∙Q(x) = 2x2∙(3x3
+ 2x2 + x + 1) será obtido utilizando a propriedade distributiva da
multiplicação, temos:
P(x)∙Q(x) = 2x2 ∙
(3x3 + 2x2 + x + 1) = 6x5 + 4x4
+ 2x3 + 2x
Lembre-se que ao efetuar a multiplicação de potências de mesma base, devemos somar os expoentes!
4 - MULTIPLICAÇÃO DE POLINÔMIOS:
Da mesma forma que o caso anterior, a multiplicação de um polinômio por outro polinômio é feita utilizando a propriedade distributiva da multiplicação, isto é, deveremos multiplicar cada termo do primeiro polinômio por cada termo do segundo.
EXEMPLO 07:
Dados os polinômios P(x) = 2x + 3 e Q(x) = 3x3 + 2x2 + x + 1,
determine o produto P(x)∙Q(x):
Resolução:
O produto P(x) ∙ Q(x) =
(2x + 3)∙(3x3 + 2x2 + x + 1), utilizando a propriedade
distributiva da multiplicação, o termo 2x multiplica todos os termos do
polinômio Q(x), e o mesmo
ocorre para o termo 3, em
P(x). Observe:
2x ∙ 3x3 = 6x4
2x ∙ 2x2 = 4x3
2x ∙ x = 2x2
2x ∙ 1 = 2x 3 ∙ 1 = 3
Assim, temos:
(2x + 3)∙(3x3 + 2x2 + x + 1) =
= 6x4 + 4x3 + 2x2 + 2x
+ 9x3 + 6x2 + 3x + 3
Observe que o grau do produto P(x)∙ Q(x) é a soma dos graus de P(x) e Q(x), isto é, 2 + 3 = 5.
Agora reduzindo os termos
semelhantes, verificamos.
P(x)Q(x)
=
EXEMPLO 08:
Agora considere os polinômios A(x)= (3x2 + 4) e B(x)= (5x² – 12x – 6).
Então para achar o produto A(x)∙B(x) = (3x2 + 4)∙(5x² – 12x – 6), devemos novamente utilizar a propriedade distributiva:
A(x)∙B(x) = (3x2 + 4)∙(5x2 – 12x – 6)
A(x)∙B(x) = 15x4 – 36x3 – 18x2 + 20x2 – 48x – 24
Reduzindo os termos
semelhantes encontramos:
A(x)∙B(x) = 15x4 – 36x3 + 2x2 – 48x – 24
Atividades:
1) Considere os polinômios
P(x) = –2x² + 5x – 2 e Q(x) = –3x³ + 2x – 1. Efetue a adição entre eles.
2) Dados os polinômios A(x) = 2x³ – 5x² – x + 21 e B(x) =
2x³ + x² – 2x + 5, determine:
a) A(x) + B(x)
b) A(x) – B(x)
3) Considere o monômio M(x) = 3x e o polinômio P(x) = 5x2 + 3x – 1, determine o resultado da multiplicação M(x)∙P(x).
4) Dados o monômio P(x) = 2x + 3 e o polinômio Q(x)
= 3x3 + 2x2 + x + 1,
determine o produto P(x) ∙ Q(x).
5)
São dados os polinômios: G = 3x² – y,
H = 5y + 3 e J = – 7x² + 2y.
Qual
é o resultado de G ∙ H – J?
(A) 15x²y
+ 7x² – 5y
(B) 15x²y + 2x² + 16y² – y
(C) 15x²y + 16x² – 5y² – 5y
(D) 15x²y + 16x² + 5y² + 5y
6) O presidente do Tabajara Futebol Clube precisa cercar o campo e quer
quantos metros de alambrado terá que comprar, sendo o comprimento desse campo
de futebol dado por 5x + 20 e sua
largura por 4x + 10 metros.
a) Calcule o perímetro desse campo?
b) Para gramar o campo, é necessário calcular a sua área, calcule-a.
Produtos Notáveis
Os produtos notáveis possuem fórmulas gerais, que, por sua vez, são a simplificação de produtos algébricos. Veja:
(x + 2)∙(x + 2) =
(y – 3)∙(y – 3) =
(z + 4 )∙(z – 4) =
Cinco casos de Produtos Notáveis
Há cinco casos distintos de produtos notáveis, a saber:
Primeiro Caso: Quadrado da soma de dois termos.
Quadrado: expoente 2;
Soma de dois termos: a + b;
Logo, o quadrado da soma de dois
termos é: (a + b)2.
Efetuando o produto do quadrado da
soma, obtemos:
(a + b)2 = (a + b) ∙ (a + b) =
=
a2 + a ∙ b + a ∙ b + b2 =
=
a2 + 2 ∙ a ∙ b + b2
Toda essa expressão, ao ser reduzida,
forma o produto notável, que é dado por:
(a
+ b)2 = a2 + 2∙a∙b + b2
Sendo assim, o quadrado da soma de
dois termos é igual ao quadrado do primeiro termo, mais duas vezes o primeiro
termo pelo segundo, mais o quadrado do segundo termo.
Exemplos:
(2
+ a)2 = 22 + 2 ∙ 2 ∙ a + a2 = 4
+ 4a + a2
(3x
+ y)2 = (3 x)2 + 2 ∙ 3x ∙ y + y2 =
9x2 +6xy + y2
Segundo Caso: Quadrado da diferença de dois termos.
Quadrado: expoente 2;
Diferença de dois termos: a – b;
Logo, o quadrado da diferença de dois
termos é: (a – b)2.
Vamos efetuar os produtos por meio da
propriedade distributiva:
(a –
b)2 = (a – b)∙(a – b)
= a2 –
a . b – a . b + b2 =
=
a2 – 2 .a . b + b2
Reduzindo essa expressão, obtemos o
produto notável:
(a
– b)2 = a2 – 2∙a∙b + b2
Temos, então, que o quadrado da
diferença de dois termos é igual ao quadrado do primeiro termo, menos duas
vezes o primeiro termo pelo segundo, mais o quadrado do segundo termo.
Exemplos:
(a
– 5c)2 = a2 – 2 ∙ a ∙ 5c + (5c)2 =
a2 – 10∙a∙c + 25c2
(p
– 2s) = p2 – 2 ∙ p ∙ 2s + (2s)2 = p2 –
4ps + 4s2
Terceiro
Caso: Produto da soma pela diferença de dois termos.
Produto: operação de multiplicação;
Soma de dois termos: a + b;
Diferença de dois termos = a – b;
O produto da soma pela diferença de dois termos é: (a + b) ∙ (a – b).
Resolvendo o produto de (a + b) ∙ (a – b), obtemos:
(a + b) . (a – b) = a2 – ab + ab – b2 = a2 + 0 + b2 = a2 – b2
Reduzindo a expressão, obtemos o
produto notável:
(a
+ b) . (a – b) = a2 – b2
Podemos concluir, portanto, que o produto da soma pela diferença de dois termos é igual ao quadrado do primeiro termo menos o quadrado do segundo termo.
Exemplos:
(2
– c) ∙ (2 + c) = 22 – c2 = 4 – c2
(3x2 –
1) ∙ (3x2 + 1) = (3x2)2 – 12 =
9x4 – 1
Quarto
caso: Cubo da soma de dois termos
Cubo: expoente 3;
Soma de dois termos: a + b;
Logo, o cubo da soma de dois termos é:
Efetuando o produto por meio da
propriedade distributiva, obtemos:
(a + b)3 = (a + b) . (a + b) . (a + b) =
=
(a2 + a ∙ b + a ∙b + b2) ∙ (a + b) =
=
( a2 + 2 ∙a ∙ b + b2 ) ∙( a + b ) =
=
a3 +2∙a2∙b + a∙b2 + a2∙b
+ 2∙a b2 + b3 =
=
a3 + 3 ∙a2∙b + 3∙a∙b2 + b3
Reduzindo a expressão, obtemos o
produto notável:
(a
+ b)3 = a3 + 3 ∙ a2 ∙ b + 3∙a∙b2 +
b3
O cubo da soma de dois termos é dado pelo cubo do primeiro, mais três vezes o primeiro termo ao quadrado pelo segundo termo, mais três vezes o primeiro termo pelo segundo ao quadrado, mais o cubo do segundo termo.
Exemplo
(3c
+ 2a)3 = (3c)3 + 3∙(3c)2 ∙2a +
3∙3c∙(2a)2 + (2a)3 = 27c3 + 54c2a
+ 36ca2 + 8a3
Quinto
caso: Cubo da diferença de
dois termos
Cubo: expoente 3;
Diferença de dois termos: a – b;
Logo, o cubo da diferença de dois
termos é: (a – b )3.
Efetuando os produtos, obtemos:
(a –
b)3 = (a – b) . (a –
b) . (a – b) =
=
(a2 - a . b - a ∙b + b2) ∙ (a – b) =
=
(a2 – 2 ∙ a ∙ b + b2) ∙ (a – b) =
=
a3 – 2 ∙ a2 ∙ b + a ∙ b2 –
a2 ∙ b + 2 ∙ a ∙ b2 – b3 =
=
a3 – 3 ∙ a2 ∙ b + 3∙ a ∙ b2 – b3
Reduzindo a expressão, obtemos o produto notável:
(a
– b)3 = a3 – 3a2b + 3ab2 –
b3
O cubo da diferença de dois termos é
dado pelo cubo do primeiro, menos três vezes o primeiro termo ao quadrado pelo
segundo termo, mais três vezes o primeiro termo pelo segundo ao quadrado, menos
o cubo do segundo termo.
Exemplo:
(x
– 2y)3 = x3 –
3 ∙ x2 ∙ 2y + 3 ∙ x ∙ (2y)2 – (2y)3 =
x3 – 6 x2y + 12xy2 – 8y3
Fatoração de polinômio
Fatoração de polinômios é um conteúdo matemático que reúne técnicas para escrevê-los em forma de produto entre monômios ou até mesmo entre outros
Todo número inteiro maior que 1 pode ser decomposto em um produto de números primos.
As técnicas usadas para fatorar polinômios – chamadas de casos de fatoração – baseiam-se nas propriedades da multiplicação, em especial na propriedade distributiva. Os seis casos de fatoração de polinômios são os seguintes:
1º caso de fatoração: fator comum em evidência
Observe, no polinômio a seguir,
que existe um fator repetindo-se em cada um de seus termos.
4x + ax
Para escrever esse polinômio na
forma de produto, coloque esse fator que se repete em
evidência. Para isso, basta fazer o processo inverso da propriedade
distributiva da seguinte maneira:
x(4 + a)
Observe que, aplicando a propriedade distributiva
nessa fatoração, teremos justamente o polinômio inicial.
Veja outro exemplo do primeiro caso de fatoração:
4x3 +
6x2
4x3 +
6x2 = 2·2xxx + 2·3xx = 2xx(2x + 3) = 2x2(2x + 3)
2° caso de fatoração: agrupamento
Pode ser que, ao colocar fatores comuns em evidência,
o resultado seja um polinômio que ainda possui fatores comuns.
Então, devemos fazer um segundo passo: colocar fatores comuns em evidência
novamente.
Assim, a fatoração por agrupamento é
uma dupla fatoração por fator comum.
Exemplo:
xy
+ 4y + 5x + 20
Na primeira fatoração, colocaremos os termos comuns em evidência da seguinte maneira:
y(x + 4) + 5(x + 4)
Observe que o polinômio resultante
possui, em seus termos, o fator comum x + 4. Colocando-o em evidência, teremos:
(x + 4)(y + 5)
3º caso de fatoração: trinômio quadrado perfeito
Esse caso, basicamente, é o contrário de produtos notáveis. Observe o produto
notável a seguir:
(x + 5)2 =
x2 + 10x + 25
Na fatoração do trinômio quadrado perfeito,
escrevemos polinômios expressos nessa forma como produto notável. Veja um
exemplo:
4x2 +
12xy + 9y2 = (2x + 3y)2
Observe que é preciso garantir que o polinômio é
realmente um trinômio quadrado perfeito para fazer esse procedimento.
O que é trinômio?
Trinômio é um polinômio que tem três monômios sem
termos semelhantes, veja exemplos:
3x2 + 2x + 1
20x3 + 5x – 2x2
2ab +5b + 3c
Nem todos os trinômios acima podem ser fatorados
utilizando o quadrado perfeito.
O que é quadrado perfeito?
Para melhor entender o que é quadrado perfeito,
veja:
Podemos considerar um número sendo quadrado perfeito? Sim, basta que esse
número seja o resultado de outro número elevado ao quadrado, por exemplo: 25 é
um quadrado perfeito, pois 52 = 25.
Agora, devemos aplicar isso em uma expressão
algébrica, observe o quadrado abaixo com lados x + y, o valor desse lado é uma
expressão algébrica.
Para calcularmos a área desse quadrado podemos seguir duas formas diferentes:
1ª forma: a fórmula para o cálculo da área
do quadrado é A = Lado2, então, como o lado nesse quadrado é
x + y, basta elevá-lo ao quadrado.
A1 = (x + y)2
O resultado dessa área A1 = (x + y)2 é um
quadrado perfeito.
2ª forma: esse quadrado foi dividido em quatro retângulos onde cada um
tem a sua própria área, então a soma de todas essas áreas é a área total do
quadrado maior, ficando assim:
A2 = x2 +
xy + xy + y2, como xy
e xy são semelhantes podemos somá-los:
A2 = x2 +2xy + y2
O resultado da área A2 = x2 +2xy + y2 é um trinômio.
As duas áreas encontradas representam a área do mesmo quadrado, então:
A1 = A2
(x + y)2 = x2 +2xy + y2
Então, o trinômio x2 + 2xy
+ y2 tem como quadrado perfeito (x + y)2.
Quando tivermos uma expressão algébrica e ela for um trinômio do quadrado
perfeito a sua forma fatorada é representada em forma de quadrado perfeito,
veja:
O trinômio x2 +2xy + y2 fatorado fica (x + y)2.
Como identificar um trinômio do quadrado perfeito?
Como já foi dito, nem todo trinômio pode ser representado na forma de quadrado
perfeito. Agora, quando é dado um trinômio como iremos identificar que é
quadrado perfeito ou não?
Para que um trinômio seja quadrado perfeito ele deve ter algumas
características:
• Dois termos (monômios) do trinômio devem ser
quadrados.
• Um termo (monômio) do trinômio deve ser o dobro das raízes quadradas dos dois
outros termos.
Veja um exemplo:
Veja se o trinômio 16x2 + 8x + 1 é um quadrado perfeito, para isso
siga as regras acima:
Dois membros do trinômio têm raízes quadradas e o dobro delas é o termo do
meio, então o trinômio 16x2 + 8x + 1 é quadrado perfeito.
Então, a forma fatorada do trinômio é 16x2 + 8x + 1 é (4x + 1)2, pois é a
soma das raízes ao quadrado.
Veja alguns exemplos:
Exemplo 1:
Dado o trinômio m2 – m n
+ n2, devemos tirar as raízes dos termos m2 e n2,
as raízes serão m e n, o dobro dessas raízes será 2∙m∙n que é diferente do termo m n (termos do meio), então esse
trinômio não é quadrado perfeito.
Exemplo 2:
Dado o trinômio 4x2 – 8xy
+ y2, devemos tirar as raízes dos termos 4x2 e y2,
as raízes serão respectivamente 2x e y. O dobro dessas raízes deve ser 2∙2x∙y = 4xy, que é diferente do termo 8xy,
então esse trinômio não poderá ser fatorado utilizando o quadrado perfeito.
Exemplo 3:
Dado o trinômio 1 + 9a2 –
6a.
Devemos, antes de usar as regras do quadrado
perfeito, colocar o trinômio em ordem crescente de expoentes, ficando assim:
9a2 –
6a + 1.
Agora, tiramos a raiz dos termos 9a2 e 1, que serão
respectivamente 3a e 1. O dobro
dessas raízes será 2∙3a1 = 6a, que é igual ao termo do meio (6a), então concluímos que o trinômio é
quadrado perfeito e a forma fatorada dele é (3a
– 1)2.
4º caso de fatoração: diferença de dois quadrados
Polinômios conhecidos como diferença de dois
quadrados possuem esta forma:
x2 –
a2
A sua fatoração é o produto notável conhecido
como produto da soma pela diferença. Observe o resultado da
fatoração desse polinômio:
x2 –
a2 = (x + a)(x – a)
5º caso de fatoração: diferença de dois cubos
Todo polinômio de grau 3 escrito
na forma x3 + y3 pode ser fatorado da
seguinte maneira:
x3 +
y3 = (x + y)(x2 – xy + y2)
6º caso de fatoração: Soma de dois cubos
Todo polinômio de grau 3 escrito
na forma x3 – y3 pode ser fatorado da
seguinte maneira:
x3 –
y3 = (x – y)(x2 + xy + y2)
Atividades:
1) Calcule:
a) (2x + 2y)2 =
b) (3x – 3y)2 =
c) (x + 5)(x – 5)=
d) (x + 3)2 =
e) (y – 2)2 =
f) (3m + 2n)(3m – 2n)=
2) Calcule a área das figuras abaixo, com suas medidas expressas
algebricamente:
a) retângulo: 2x + 1 e 2x – 1;
b) quadrado: (5x – 3)
c) triângulo: (2x – 4)
3) Sabe-se que a área de uma piscina retangular é expressa por 4x2 – 64, se o comprimento da
piscina é expresso por 2x + 8, qual a expressão da largura dessa piscina?
4) Identifique se os trinômios são quadrados perfeitos e expresse sua
forma fatorada:
a) 25x2 + 90x + 81
b) x2 – 8x + 16
c) x2 + 10x + 25
d) 4x2 – 16x + 64
5) Observe
as igualdades abaixo.
(I)
(x + 3)² = x² + 9
(II) (y
– 4).(y + 4) = y² – 16
(III) (2x
– 5)² = 4x² – 20x + 25
Quais
dessas igualdades estão corretas?
(A)
I e II, apenas.
(B) I e III, apenas.
(C) II e III, apenas.
(D) I, II e III.
6)
A forma fatorada da expressão 6ab + 15a –
2b – 5 é:
(A) (3a
– 1)∙(2b – 5)
(B)
(3a – 1)∙(2b + 5)
(C) (3a
+ 1)∙(2b – 5)
(D) (3a
+ 1)∙(2b + 5)
7) (ENEM-2016) Um terreno
retangular de lados cujas medidas, em metro, são x e y será cercado para a construção
de um parque de diversões. Um dos lados do terreno encontra-se às margens de um
rio. Observe a figura.
Para cercar todo o terreno, o
proprietário gastará R$ 7.500,00. O material da cerca custa R$ 4,00 por metro
para os lados do terreno paralelos ao rio, e R$ 2,00 por metro para os demais
lados.
Nessas condições, as dimensões
do terreno e o custo total do material podem ser relacionados pela equação:
(A) 4(2x + y) = 7.500
(B) 4(x + 2y) = 7.500
(C) 2(x + y) = 7.500
(D) 2(4x + y) = 7.500
(E)
2(2x + y) = 7.500
Função Quadrática
Sejam dados os coeficientes reais a, b e c, com a ≠ 0. A função definida por f(x) = ax2 + bx + c é denominada função quadrática.
As funções quadráticas têm aplicações em áreas variadas, como a física, a economia, a engenharia, a biologia e a geografia.
O problema abaixo mostra o emprego de uma função quadrática à descrição da trajetória de uma bola.
Problema 1. Um golfista dá uma tacada que faz sua bola descrever
uma trajetória na qual a altura, em metros, é dada pela função f(x) = −0,008x2 + x, em que x é a distância horizontal da bola, em
metros, medida a partir de sua posição antes da tacada.
Quando a bola está a uma
distância horizontal x do ponto de
partida, sua altura é f(x).
a) Determine a altura da bola
quando ela está a uma distância horizontal de 40 m de seu ponto de partida.
b) Com base em uma tabela de
pontos, trace a trajetória da bola no plano Cartesiano.
c) Determine a que distância
do ponto de partida a bola cai no chão.
Solução:
a) A altura da bola quando ela
está a uma distância horizontal de 50 m de sua posição original é dada por
f(40) = −0,008 ⋅
402 + 40 = 27,2.
Logo, a bola está a uma altura de 27,2 m.
b) A Tabela abaixo fornece uma lista de pares ordenados obtidos a partir da definição de f.
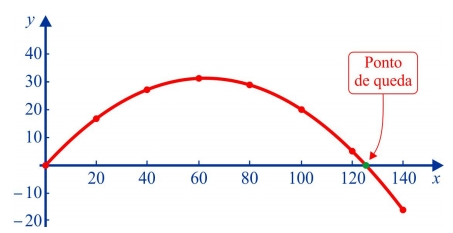
Com base nesses pontos, traçamos o gráfico abaixo, que mostra a trajetória descrita pela bola:
c) Observando o gráfico,
concluímos que a bola toca o solo a cerca de 125 metros de seu ponto de
partida. Para determinar com exatidão a coordenada horizontal desse ponto, basta
lembrar que dizer que a bola está sobre o solo é o mesmo que afirmar que sua
altura é zero.
Assim, temos f(x) = 0, ou seja,
−0,008x2 + x = 0 ⇒
x(−0,008x
+ 1) = 0.
Assim temos, as raízes dessa equação devem satisfazer:
x = 0 ou −0,008x + 1 = 0.
Nesse último caso, temos:
Logo, os pontos em que a bola
toca o solo são aqueles nos quais x = 0 m (ponto de partida) e x = 125 m, que é a
distância horizontal entre o ponto de partida
e o ponto de queda da bola.
A curva mostrada no trecho entre x = 125 e x = 140, no qual os valores de f(x) são negativos. Esse trecho foi usado apenas para completar a trajetória até o ponto de queda, não implicando que, na prática, a bola tenha tido uma altura negativa, o que só aconteceria se ela fosse enterrada no solo.
É importante notar que uma função quadrática pode ser fornecida em outro formato que não aquele apresentado no quadro acima, como mostram os exemplos a seguir.
Problema 2: Converta as funções abaixo ao formato f(x) = ax2 + bx + c.
a) f(x) = 2(x − 1)(x + 3)
b) f(x) = −3(x − 4)2
+ 6
Solução.
a) Aplicando a propriedade distributiva, podemos escrever:
2(x − 1)(x +
3) = 2(x2 − x + 3x − 3) = 2x2 + 4x − 6.
Logo, f(x) = 2x2 + 4x − 6.
b) Usando a regra do quadrado da soma (ou a propriedade distributiva
mais uma vez), obtemos:
−3(x − 4)2 + 6 = −3(x2 − 8x + 16) + 6 = −3x2
+ 24x − 48 + 6 = −3x2 + 24x − 42.
Assim, f(x) = −3x2 + 24x − 42.
Gráfico
das funções
quadráticas
O gráfico
de uma função quadrática tem um formato característico – similar a uma letra
“U” mais aberta –, e é chamado parábola.
A Figura abaixo mostra duas
parábolas típicas:
Observando as curvas dos
gráficos, notamos que a função quadrática tem um ponto de mínimo ou um ponto
de máximo local. A esse ponto especial da parábola damos o nome de vértice.
Além disso, toda parábola é
simétrica a uma reta vertical que passa por seu vértice. Essa reta vertical é
denominada eixo de simetria.
Outra característica
importante de parábola é a sua concavidade,
que é a lado para o qual a curva se abre. Na primeira curva mostra uma parábola
com concavidade para cima, enquanto a
segunda curva mostra uma parábola com concavidade
para baixo.
Note que há uma relação entre
a concavidade e o sinal do coeficiente a. Se a > 0, a parábola tem concavidade
para cima. Por outro lado, a concavidade
é para baixo se a < 0.
O parâmetro a também controla a abertura da parábola. Quanto maior for o valor absoluto desse parâmetro, menor será a abertura, e vice-versa, como ilustra o gráfico abaixo:
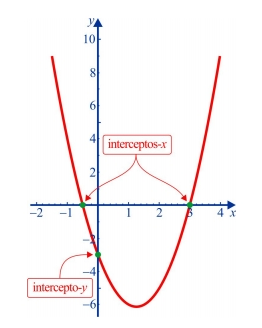
Por sua vez, o coeficiente c da função quadrática determina o intercepto-y da parábola, pois, tomando x = 0, temos:
f(0) = a ⋅
02 + b ⋅
0 + c = c.
Já os interceptos-x da parábola correspondem às raízes da equação f(x) = 0, que é equivalente à equação quadrática
ax2 + bx + c = 0.
Resolução de Equação de 2º grau ou zero da função quadrática
A ideia principal do método para resolver uma equação do tipo ax2 + bx + c = 0, com a ≠ 0, é essa:
ü Se
ax2 + bx + c for um
quadrado perfeito, podemos fatorá-lo na forma (d + e)2 ou (d –
e)2, cuja resolução é simples. Acompanhe a resolução de 16x2 + 8x + 1 = 16.
Fatoramos: 16x2 + 8x + 1 em (4x + 1)2, escrevemos (4x + 1)2 = 16
e obtemos 4x + 1 = 4 ou 4x + 1 = –4.
Resolvendo as equações acima,
temos: x = 3/4 ou x = –5/4.
S = {−5/4, 3/4}.
ü Se
o trinômio não for um quadrado perfeito, para resolver a equação proposta
devemos completar um quadrado perfeito a partir da expressão dada. Acompanhe o
quadro abaixo:
Com isso, obtemos a fórmula
geral de resolução, na qual b2
– 4ac é o discriminante, também
representado pela letra grega maiúscula ∆ (“delta”).
Essa expressão é conhecida
como fórmula de Bhaskara, em homenagem ao matemático indiano Bhaskara Akaria (1114-1185).
Exemplo: Dada a função quadrática f(x) = 2x2 − 5x − 3, determine os interceptos de seu gráfico com os eixos coordenados.
Solução:
• O intercepto-y da parábola é dado pelo coeficiente c, cujo valor é −3.
• Para obter os interceptos-x, devemos resolver a
equação 2x2 − 5x − 3 = 0.
Nesse caso, o discriminante vale
∆ = b2 − 4ac = (−5)2
− 4 ⋅
2 ⋅
(−3) = 25 + 24 = 49.
Como ∆ > 0, sabemos que o
gráfico intercepta o eixo-x em dois
pontos.
Recorrendo, então, à fórmula de Bhaskara, obtemos:
Logo, os interceptos são:
O gráfico obtido será:
Desta forma, podemos analisar acerca do papel do discriminante:
∆ = b2 − 4ac
do polinômio quadrático, numa função quadrática e podemos dizer que a parábola:
• intercepta o eixo-x em dois pontos se
∆ > 0;
• intercepta o eixo-x em um ponto se ∆ = 0;
• não
intercepta o eixo-x se ∆ < 0.
Atividades:
1) Um terreno, que tem a forma de um quadrado, foi reduzido da maneira indicada na figura abaixo, para dar lugar a uma calçada com 2 m de largura. Ao final, sua área passou a ser de 484 m². Qual era a medida do lado do terreno original?

2) Resolva as equações abaixo:
a) x2 = 4
b) (2x – 3)2 = 25
c) 25x2
+ 90x + 81 =0
d) x2 – 2x – 15 = 0
e) 2x2 + 3x + 1 = 0
3) O produto entre dois números naturais consecutivos é 156. A soma desses dois números é:
(A) 1. (B) 25. (C) 27. (D) 156.
4) Antônio, com 20m de cerca,
construiu um cercado retangular de 32 m² de área, utilizando seu muro como um
dos lados. Quais as medidas dos lados desse cercado retangular?
5) Para presentear os colegas
no natal, Ana comprou alguns exemplares de um livro por R$ 540,00. Por ter
obtido um desconto de R$ 15,00 no preço de cada exemplar do livro, ela conseguiu
comprar 3 exemplares a mais do que previra originalmente. Com o desconto
concedido, quantos exemplares desse livro Ana comprou?
6) Quero fazer um cercado
retangular com 22 m² de área. O material que possuo dá para erguer 26 m de
cerca. Que medidas devem ter os lados do meu cercado retangular?
7) O dono da marcenaria, que
fabrica certo tipo de armário, verificou que o número N de armários que ele pode fabricar por mês depende do número x de funcionários trabalhando na
marcenaria e que essa dependência é dada pela igualdade N = x2 + 2x. Qual é o número de funcionários necessários
para a marcenaria fabricar 168 armários em um mês?
8) Uma pessoa distribui 240
balas para um certo número de crianças. Se cada criança receber uma bala a
menos, o número de balas que cada criança vai receber será igual ao número de crianças.
Qual é o número de crianças?
9) Defina uma função f(x) que forneça a área da região destacada na figura, lembrando que a área de um retângulo de lados b e h é bh.
10) Dada a função
f(x) = x2 − 3x:
a) determine algebricamente os
pontos nos quais f(x) = 0;
b) determine algebricamente os pontos nos quais f(x) = −2;
c) esboce
o gráfico da função no plano coordenado, indicando os pontos que você obteve no
item (b);
d) determine graficamente as
soluções da inequação f(x) ≥ −2.
11) Dada a função f(x) = 5x − 2x2:
a) determine algebricamente os
pontos nos quais f(x) = 0;
b) determine algebricamente os
pontos nos quais f(x) = 2;
c) esboce o gráfico da função
no plano coordenado, indique os pontos que você obteve no item (b);
d) determine graficamente as
soluções da inequação f(x) ≥ 2.
11) Dada a função f(x) = −2x2 + 9x:
a) determine algebricamente os
pontos nos quais f(x) = 0;
b) determine algebricamente as
soluções da inequação f(x) ≥ 9;
c) determine algebricamente o
ponto de mínimo ou máximo de f;
d) esboce o gráfico da função
no plano coordenado.
12) Dada a função f(x) = −3x2 + 15x:
a) determine algebricamente os
pontos nos quais f(x) = 0;
b) determine algebricamente as
soluções da inequação f(x) ≥ 12;
c) determine algebricamente o
ponto de mínimo ou máximo de f;
d) esboce o gráfico da função
no plano coordenado.
13) Dada a função f(x) = 15x2
+ x – 2:
a) determine algebricamente os
pontos nos quais f(x) = 0;
b) determine algebricamente as
soluções da inequação f(x) ≤ −2;
c) determine algebricamente o
ponto de mínimo ou máximo de f.
14) Esboce o gráfico e
determine o ponto de mínimo ou máximo de cada função.
a) f(x) =
(x − 1)(x + 2)
b) f(x) =
(−3 − x)(x + 3)
c) f(x) =
x2 − 3x + 4
d) f(x) =
−2x2 + 3x + 2
e) f(x) =
4x + x2
f) f(x) =
−x2 − 4
g) f(x) =
(x − 4)(x + 1)
q = 400 – 100p,
na qual q representa a quantidade de pães especiais vendidos diariamente e
p, o seu preço em reais.
(A) R$ 0,50 ≤ p < R$ 1,50
(B) R$ 1,50 ≤ p < R$ 2,50
(C) R$ 2,50 ≤ p < R$ 3,50
(D) R$ 3,50 ≤ p < R$ 4,50
(E) R$ 4,50 ≤ p < R$ 5,50
16) (ENEM-2015) Um meio de transporte coletivo que vem ganhando espaço no Brasil é a van, pois realiza, com relativo conforto e preço acessível, quase todos os tipos de transportes: escolar e urbano, intermunicipal e excursões em geral.
O dono de uma van, cuja capacidade máxima é de 15 passageiros, cobra para uma excursão até a capital de seu estado R$ 60,00 de cada passageiro. Se não atingir a capacidade máxima da van, cada passageiro pagará mais R$ 2,00 por lugar vago.
Sendo x o número de lugares vagos, a expressão que representa
o valor arrecadado V(x), em reais, pelo dono da van, para uma viagem até a capital é
(A) V(x)
= 902x
(B) V(x)
= 930x
(C) V(x)
= 900 + 30x
(D) V(x)
= 60x + 2x²
(E) V(x)
= 900 − 30x − 2x²
Qual o tempo mínimo de espera, em minutos, após se
desligar o forno, para que a porta possa ser aberta?
(A)
19,0
(B)
19,8
(C)
20,0
(D)
38,0
(E)
39,0
18) (ENEM-2016) Para evitar uma epidemia, a Secretaria de Saúde de uma cidade dedetizou todos os bairros, de modo a evitar a proliferação do mosquito da dengue. Sabe-se que o número f de infectados é dado pela função f(t) = ̶ 2t² + 120t (em que t é expresso em dia e t = 0 é o dia anterior à primeira infecção) e que tal expressão é válida para os 60 primeiros dias da epidemia.
A Secretaria de Saúde decidiu que uma segunda dedetização deveria ser feita no dia em que o número de infectados chegasse à marca de 1 600 pessoas, e uma segunda dedetização precisou acontecer.
A segunda dedetização começou no:
(A) 19º dia.
(B) 20º dia.
(C) 29º dia.
(D) 30º dia.
(E) 60º dia.
Para determinar o custo da
obra, um engenheiro deve calcular a área sob o arco parabólico em questão.
Usando o eixo horizontal no
nível do chão e o eixo de simetria da parábola como eixo vertical, obteve a
seguinte equação para a parábola:
ü y = 9 – x2 , sendo x e y medidos em metros.
Sabe-se que a área sob uma
parábola como esta é igual a 2/3 da área do retângulo cujas dimensões são,
respectivamente, iguais à base e à altura da entrada do túnel.
Qual é a área da parte frontal
da tampa de concreto, em metro quadrado?
(A) 18
(B) 20
(C) 36
(D) 45
(E) 54















Nenhum comentário:
Postar um comentário