Prismas

Área de um Sólido Geométrico

Para aquisição de tintas para pintar um ambiente, é necessário informar quantos metros quadrados deseja pintar para saber quanto de tinta é necessário comprar. Essa grandeza apresentada é a área de um ambiente, como uma sala, um quarto, que podem ser representadas como sólidos geométricos.

Tomemos um exemplo:

Simão precisa fazer o cálculo da quantidade de tinta para pintar o seu quarto. Para isso ele decidiu medir todo o quarto.

Verificou que o quarto mede aproximadamente 3,5 m por 4 m no piso e tem 2,9 m de altura. No quarto há ainda uma porta de 72 cm por 2,1 m e uma janela de 1,9 m por 90 cm.

Considerando as informações apresentadas na lata de tinta a seguir e as dimensões do quarto, quantas latas dessa tinta Simão deve comprar para passar duas demãos de tinta no quarto (as informações da lata se referem a apenas uma demão de tinta)?

 

A prescrição da lata informa que ela pinta 100 m².

Logo, percebe-se que uma lata basta para fazer duas demãos. 

Estudemos como calcular esse tipo de modelo.

Um quarto tem formato de cúbico ou um prisma retangular reto (paralelepípedo), dependendo de suas dimensões.

Podemos destacar de um prisma qualquer três tipos de áreas, a saber:

a) área da base:

A característica de um prisma é sua base (fundo ou chão) ter formato de polígono e sua face superior (tampa ou teto) tem o formato do mesmo polígono da base.

No exemplo do quarto, o chão tem formato de um retângulo e por consequência o teto tem o mesmo formado, o que caracteriza um prisma.

Para calcular a área da base, calcula-se a área do polígono que a base é formada.

Assim, se a base de um prisma for um quadrado, a área da base será a área do quadrado, bem como se for formado por um retângulo, triângulo, pentágono, hexágono, será a área de tal polígono.

Como, no exemplo de pintura do quarto, não se pinta o chão, a área da base servirá para saber a área que deve ser pintado o teto do quarto.

 

 

b) área lateral:

A característica de um prisma é que as faces laterais têm formato de retângulos e terão tantos retângulos quantos forem o número de lados do polígono da base.

No exemplo do quarto, como o polígono da base tem quatro lados, teremos 4 faces laterais (retângulos).

A área lateral de um prisma é calculada somando cada área dos retângulos que formam essa lateral.

Assim, se a base de um prisma for um quadrado, a área lateral será a soma da área dos quatro retângulos das laterais, bem como se for formado por um retângulo, triângulo, pentágono, hexágono, será a soma de cada área do número de retângulo que for formado o polígono da base.

No quarto, as faces laterais são as paredes, daí calcula-se a área de cada parede e soma-se para obter a área lateral a ser pintada.

 

c) área total:

Um prisma é formado de base, face superior e faces laterais.

A área total de um prisma será a soma das áreas de todas as faces do sólido.

Assim, se a base for quadrangular, soma-se a área da base, a área da face superior e as áreas das quatro faces laterais.

Na pintura do quarto, não é necessário calcular a área total, pois não se pinta o chão de um quarto, ou pode-se calcular a área total e retirar a área da base. 

Exemplos:

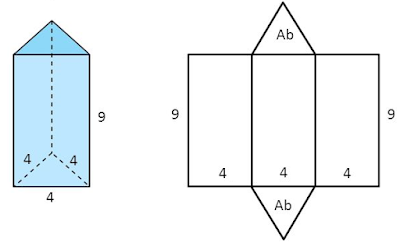
1) Calcular a área lateral do prisma reto de base triangular com as medidas dadas abaixo: 

Vejamos que por ser um prisma de base triangular, há 3 faces laterais retangulares, como só exemplo só solicita o cálculo de uma área lateral, basta calcularmos uma única vez: 8 x 6 = 48 cm².

Como cada face lateral tem área de 48 cm², para calcular a área lateral (A_l) do prisma, soma-se as três áreas e temos:

A_l = 3 x 48 = 144 cm².

 

2)  Calcular a área total do prisma reto de base triangular com as medidas das acima:

Para calcular a área total, já temos o valor da área lateral, temos que agora calcular a área da base, que será o mesmo valor da área da face superior.

Como, a base é um triângulo equilátero, para calcular vamos recorrer à consequência do Teorema de Pitágoras:

 Área de um triângulo equilátero:

  

com l lado do triângulo.

 A área do triângulo da base (A_b) é: 

 

(Perceba que a área da base é um valor irracional, conhecida como uma medida incomensurável, que não se pode medir com um instrumento de medida como uma régua e seu valor será expresso dessa forma de radical, a efeito de demonstração. Somente sendo substituído o radical por um valor aproximado quando pedido no exercício ou segundo a necessidade no contexto)

Finalmente, o valor da área total (A_t) será a soma da área lateral com o dobro da área da base:

A_t = A_l + 2∙A_b

A_t = 144 + 2 x 16

A_t = 144 + 32 cm²

 

Uma boa aproximação para   é 1,7; fazendo a substituição na área total apresentada acima, temos:

A_t = 144 + 32 x 1,7 = 144 + 54,4 = 198,4 cm²(aproximadamente).

 

3) Calcular a área total de um paralelepípedo de dimensões 3 cm, 4 cm e 7 cm, de comprimento, largura e altura, respectivamente, como na figura abaixo:

Nesse caso, temos 6 faces: duas bases retangulares e quatro laterais, sendo uma frente e outro atrás.

A base tem dimensões 3 cm e 4 cm.

Então, área da base é:

A_b = 3 x 4 = 12 cm².

 

As laterais esquerda e direita 4 cm e 7 cm, e tanto na frente quando na parte de trás, 3 cm e 7 cm.

Então a área lateral é:

A_l = 2 x 4 x 7 + 2 x 3 x 7

A_l = 56 + 42

A_l = 98 cm²

 

Finalmente, a área total será:

A_t = 98 + 2 x 12 = 98 + 24 = 122 cm².

 

 

 

Volume de um prisma: 

Você já deve ter percebido que as embalagens nos supermercados são caixas (caixa de leite, de suco, etc). Evidentemente, os fabricantes querem que o volume que elas contêm seja o definido (por exemplo, 1 L) com o mínimo gasto de material possível. Vejamos dois exemplos de caixas: 

Ambas contêm o mesmo volume (1.000 cm³ = 1 litro), porém, na primeira caixa utilizou-se, em sua construção, uma área total de:

700 cm² (2 x 10 x 5 + 4 x 5 x 20),

enquanto que na segunda utilizou-se uma área total de:

1.186,40 cm² (2 x  4 x 25 + 20 x 4 + 20 x 25 + 20 x 25,32).

Logo, a primeira caixa é a mais utilizada, pois oferece o mesmo volume com menor custo.

 

Como calcular o volume de algum objeto que possua o formato de um prisma reto?

Já vimos que para calcular o volume de um paralelepípedo, como uma piscina de base retangular, basta multiplicar as três dimensões: comprimento, largura, altura.

Agora um prisma de outra base segue o mesmo raciocínio, de produto de três dimensões. Mas da seguinte forma:

Volume (V) de um prisma qualquer será o produto da área da base (A_b) pela altura (H):

V = A_b ∙ H

 

Vejamos, como calcular o volume da caixa de base retangular acima:

A_b = 10 x 5 = 50 cm²

H = 20 cm

V = 50 x 20 = 1.000 cm³.

 

Agora, calculando o volume da caixa de base triangular:

A_b = (25 x 4) / 2 = 100 / 2 = 50 cm²

H = 20 cm

V = 50 x 20 = 1.000 cm³.

 

Confirmado, assim que as duas caixas possuem o mesmo volume e mesma capacidade de 1 litro, mesmo com formato e dimensões diferentes.

 

Exemplo:

1) Um prisma de base triangular regular possui 8 cm de aresta da base e 6 cm de aresta lateral, adote  ≈ 1,7. Calcule o volume desse prisma. 

Temos a área da base:

 

Como a altura H = 6 cm então o volume será:

V = 16 x 6 = 96 cm³

 

Substituindo o radical com a aproximação indicada, temos:

V = 96 x 1,7 =163,2 cm³.

 

Atividades: 

1) Calcule a área total de um cubo cuja a aresta da base mede 6 cm. 

2) Dado um prisma triangular regular reto, com dimensões cuja aresta da base e lateral medem respectivamente 4 cm e 9 cm, calcule:

a) A área da base.

b) A área lateral. 

3) Um paralelepípedo retângulo possui dimensões, 10 cm, 5 cm e 12 cm, qual é a área total desse paralelepípedo?

 

4) Um prisma de base triangular regular possui 3 cm de aresta da base e 8 cm de altura, calcule o volume desse prisma.

 

5) Um prisma de base triangular regular possui 4 cm de aresta da base e 10 cm de aresta lateral, adote   ≈ 1,7. Calcule o volume desse prisma.

Paralelepípedo retângulo e Cubo I

1) As arestas de um paralelepípedo retângulo medem 1dm, 3dm e 4dm. Calcule:

a) a área total;

b) o volume;

c) a capacidade.

 

2) Uma caixa de fósforo possui as dimensões indicadas na figura abaixo.

Sabendo-se disso, calcule:

a) a área da base; 

b) a área lateral; 

c) a área total; 

d) o volume.

 

3) Quantos litros de água é possível encher uma caixa de forma cúbica de aresta 5 m?

 

Paralelepípedo retângulo e Cubo II

1) Uma piscina construída num terreno tem 6 m de comprimento, 3 m de largura e 2 m de profundidade.

a) Qual a área do terreno que ela ocupa?

b) Qual a quantidade de água é necessária para encher a piscina?

 

2) As dimensões de um paralelepípedo retângulo são 3 cm,  x cm e 5 cm e seu volume é 60 cm³.

a) determine o valor de x da aresta desconhecida;

b) calcule sua área total.

 

3) A área total de um cubo é 96 cm².

a) calcule o valor da área de cada face;

b) calcule o valor da aresta desse cubo;

c) calcule o seu volume.

 

4) Numa caixa d’água cúbica cabe 8.000 litros. Qual a área mínima que deve ser reservada para se colocar esta caixa num ambiente?

 

5) Um cubo tem 216 cm² de área total. Qual a medida do volume desse cubo?

  

Prisma

1) Exprima em m³ a medida do volume de um prisma de base regular cuja medida da área da base é 65 m² e cuja medida da altura é 20 m.

 

2) Num prisma triangular reto as arestas da base medem 3 cm, 4 cm e 5 cm e uma aresta lateral mede 10 cm. Calcule a área total desse prisma.

 

3) Num prisma de base hexagonal regular, as medidas das arestas da face são 2 cm na base e 3 cm na altura. Calcule:

a) a área lateral; 

b) a área da base; 

c) a área total; 

d) o volume.

 

4) Calcule o volume de um prisma hexagonal regular sabendo que perímetro de sua base é igual a 24 cm e que sua altura é igual a 8 cm.

5) (FEI) De uma viga de madeira de seção quadrada de lado l = 10 cm extrai-se uma cunha de altura h = 15 cm, conforme a figura. 

O volume da cunha é:

     (A) 250 cm³.

     (B) 500 cm³.

      (C) 750 cm³.

     (D)1000 cm³.

     (E) 1250 cm³.

Exercícios Diversos:

1) Como consequência do Teorema de Pitágoras, a área de um triângulo equilátero é dado como 

A = , sendo l a medida do lado do triângulo. 

A figura seguinte representa a planificação de um prisma. 

Usando  ≈ 1,7; se a medida de cada um dos segmentos é 2 cm então medida da área total é:

        (A) 12 cm²

        (B) 15,40 cm²

        (C) 17 cm²

        (D) 17,50 cm²

2) A figura seguinte representa a planificação de um prisma. 

Se a medida de cada um dos segmentos AB, BC, ou CD é 3, então a razão entre o volume e a área lateral do prisma é:

        (A) 0,75

        (B) 1,5

        (C) 2

        (D) 1

3) O prisma triangular representado na figura abaixo tem como base um triângulo equilátero, e suas faces laterais são quadrados de medida  cm. 

O volume desse prisma é:     

        (A) 2,25 cm³    

        (B) 2,3 cm³

        (C) 2,5 cm³     

        (D) 3 cm³

4) Um chocolate é vendido no formato de prisma triangular regular, conforme mostra a figura.

A aresta da base desse prisma é 5 cm e sua altura mede 18 cm. Utilizando  = 1,7 o volume desse chocolate é:

        (A) 191,25 cm³      

        (B) 200 cm³        

        (C) 250 cm³     

        (D) 265 cm³

5) Um reservatório de água tem a forma de um cubo com capacidade para 1.000 m³ de água. Com o objetivo de aumentar sua capacidade, devido ao crescimento populacional, dobrou-se sua largura e triplicou-se sua altura. A capacidade do novo reservatório, em metros cúbicos, passou a ser de:

        (A) 2.000

        (B) 3.000

        (C) 4.500

        (D) 6.000

6) Os cubos seguintes têm, respectivamente arestas 1, 2 e 3.

  

a) Calcule o volume de cada um dos cubos.

b) Calcule a diagonal de cada cubo.

7) Celina desenhou um paralelepípedo retângulo, como mostra a figura abaixo.

Qual é a medida da área total desse paralelepípedo?

        (A) 128 cm².   

        (B) 160 cm².  

        (C) 192 cm².   

        (D) 256 cm².   

8) Uma caixa de sabão em pó, possui as medidas representadas no desenho abaixo.

Qual é a medida da área da superfície dessa caixa?

        (A) 180 cm². 

        (B) 250 cm². 

        (C) 500 cm². 

        (D) 750 cm².

9) Para economizar papelão, um fabricante de sabão em pó mudou as dimensões da embalagem de 1 kg. As duas embalagens têm o formato de um paralelepípedo retângulo e suas dimensões estão indicadas no desenho abaixo.

Considerando-se as medidas dadas e apenas a área externa das caixas, a economia de papelão que essa mudança resultou para a empresa, por caixa, foi de:

        (A) 12 cm²  

        (B) 60 cm²  

        (C) 100 cm²   

        (D) 200 cm²

10)  Uma fábrica produz vários modelos de malas. Um dos modelos mais vendidos tem o espaço interno no formato de um prisma retangular, cujas dimensões estão representadas na figura abaixo.

Qual é a capacidade máxima, em cm³, dessa mala?

        (A) 4.316. 

        (B) 8.632. 

        (C) 14.880. 

        (D) 44.640.

11) Uma caixa retangular foi lacrada com uma fita adesiva que transpassou o centro de todas as suas faces, conforme ilustrado na figura abaixo. Observe as dimensões dessa caixa.

O comprimento de fita gasto para lacrar essa caixa foi:

        (A) 2 metros.      

        (B) 1,8 metros.  

        (C) 1 metro.   

        (D) 90 centímetro.

11) Uma aranha teceu uma teia que coincide com a diagonal de uma caixa retangular partindo do ponto P em direção ao ponto Q, conforme o desenho abaixo.

Qual é o comprimento dessa teia?

        (A) 105 cm. 

        (B) 125 cm. 

        (C) 160 cm. 

        (D) 205 cm.

12) Um canudinho de refrigerante foi colocado dentro de uma caixa em forma de paralelepípedo retângulo. Suas extremidades encostam exatamente nos vértices P e Q dessa caixa, como mostra a figura abaixo.

Qual é a medida do comprimento desse canudinho?

        (A) 41 cm.    

        (B) 32 cm.    

        (C) 25 cm.     

        (D) 21 cm.

13) Observe os desenhos em cinza nas malhas quadriculadas abaixo. Os quadradinhos dessas malhas possuem lado de medida igual a 1 cm.

Qual desses desenhos representa a planificação de um bloco retangular de 3 cm de altura cuja base é um quadrado de lado 1 cm?

14) Uma empresa precisa fabricar embalagens com capacidade de um litro. Foram apresentadas três propostas para as embalagens:

1ª proposta: no formato de um cubo de aresta 10 cm.

2ª proposta: na forma de um paralelepípedo de dimensões 5 cm, 5 cm e 40 cm

3ª proposta: na forma de paralelepípedo de arestas 5 cm, 10 cm e 20 cm.

Qual das três propostas utiliza menos material.

14) Você deve ter observado que várias marcas de sabão em pó tiveram uma mudança na embalagem de 1kg: passaram de um paralelepípedo "mais estreito e alto" para um "mais largo e baixo".

As embalagens têm medidas aproximadamente iguais a:

embalagem antiga: 4,8 cm x 16,8 cm para a base e 24 cm para a altura

embalagem nova: 19 cm x 7 cm para a base e 14,5 cm para a altura

Isso pode despertar a curiosidade: teria sido o motivo puramente estético ou houve intenção das empresas de procurar menor custo para as embalagens dos produtos, uma vez que o custo incide diretamente sobre o lucro final?

Primeiramente, pode-se fazer o cálculo do volume dos paralelepípedos das duas embalagens para verificar se ficara mantido:

4,8 x 16,8 x 24 cm³ = 1935,36 cm³

19 x 7 x 14,5 cm³ = 1928,5 cm³

Logo, a menos de aproximações nas medidas, podemos supor o volume mantido e suficiente para embalar 1kg do produto.

Agora, os cálculos das áreas superficiais dos paralelepípedos, em cm²: 

Embalagem antiga	Embalagem nova
24 x 16,8 x 2 = 806,40 16,8 x 4,8 x 2 = 161,28 4,8 x 24 x 2 = 230,40 Total = 1.198,08 cm2	19 x 14,5 x 2 = 551 19 x 7 x 2 = 266 7 x 14,5 x 2 = 203 Total = 1.020 cm2

Bingo! A caixa atual utiliza menos material para ser confeccionada que a caixa antiga.

Considerando que a população do Brasil seja aproximadamente 180 milhões de habitantes e supondo que um terço dessa população use uma caixa de sabão por mês, isso resultaria numa economia de:

60.000.000 x (1.198,08  1.020) cm² = 10.684.800 000 cm² = 1.068.480 m² de papelão por mês.

Aprofunde-se: