Já vimos que as equações quadráticas cujo discriminante é negativo – ou seja, ∆ < 0 – não têm solução real.
Uma equação quadrática simples que não possui raiz real é x2 + 1 = 0, pois, subtraindo 1 dos dois lados da equação, obtemos
x2 = −1,
e
não há um número real cujo quadrado valha −1.
Dificuldade
semelhante ocorre com equações cúbicas (do terceiro grau), quárticas (do quarto
grau) ou que envolvam polinômios de maior grau.
Para
contornar o inconveniente de não ser possível encontrar raízes reais para todas
as equações polinomiais, os matemáticos inventaram o conjunto dos números
complexos, representado por .
.
Nesse
conjunto, há um número especial, denominado unidade imaginária, ou simplesmente
i, que é definido por
de
modo que
i2 = −1.
Usando
a unidade imaginária, podemos resolver a equação quadrática acima fazendo
x2 + 1 = 0
x2 = −1
Assim,
a equação tem duas soluções, que são x1
= i e x2 = −i.
Consideremos,
agora, a equação x2 + 9 = 0.
Nesse
caso, seguindo a mesma ideia apresentada acima, escrevemos
x2 + 9 = 0
x2 = −9
Assim,
se admitirmos a existência de podemos dizer que a
equação tem duas soluções,
podemos dizer que a
equação tem duas soluções,
embora nenhuma delas seja
real.
Na
verdade, notando que
(3i)2 = 32 ∙ i2 = 9(−1) = −9, e (−3i)2
= (−3)2 ∙ i2
= 9(−1) = −9,
concluímos que as raízes da equação são os números complexos
x1 = 3i e x2
= −3i.
Raiz quadrada de números negativos
Vejamos
como obter a raiz quadrada de um número real negativo qualquer:
Dado um número real positivo b,
Entretanto,
damos preferência à forma i √ b para deixar claro que o termo i não está dentro
da raiz.
Observe que
Logo, a regra do produto de raízes de números reais, que diz que
quando a
≥ 0 e b ≥ 0, também pode ser
aplicada quando a ≥ 0 e b < 0 (ou a < 0 e b ≥ 0).
Porém,
essa regra não é válida quando os dois termos são negativos, ou seja, não se
pode dizer que
Para obter o resultado correto nesse caso, devemos seguir o que foi apresentado no quadro acima e escrever
Esse
exemplo ilustra o motivo principal de os matemáticos adotarem a unidade
imaginária i. Sem ela, os erros no
cálculo de produtos de raízes quadradas de números negativos poderiam ser
frequentes.
Exemplos:
Raízes quadradas de números reais negativos
Definição de Número Complexo
Para
estender os conceitos vistos acima a todas as equações polinomiais, definimos
os números complexos conforme mostrado no quadro abaixo.
Exemplo:
a) 5 + 3i é um número complexo com parte
real 5 e parte imaginária 3.
b) 7 − 2i é um número complexo com parte
real 7 e parte imaginária − 2.
c)
3/4 – 4/5 i é um número complexo com parte real 3/4 e parte imaginária −4/5 .
d) 4i é um número complexo com parte real 0
e parte imaginária 4.
e)
−3 é um número complexo com parte real −3 e parte imaginária 0.
Por
sua vez, os números reais – como o valor −3 citado no item (e) – podem ser
vistos como números complexos sem a
parte imaginária.
Assim,
sendo, o conjunto dos números complexos contém todos os números reais, ou seja, 
Os números complexos são empregados em diversos ramos da matemática, da física e da engenharia. Entretanto, sua aplicação mais imediata é a solução de equações polinomiais, como mostra o exemplo abaixo.
O discriminante
dessa equação é
∆ = (−6)2 − 4 ⋅ 1 ⋅ 13 = 36 − 52 = −16.
∆
< 0, obtemos:
Logo, apesar de não haver solução real, a equação tem duas raízes complexas, que são:
Note
que, quando ∆ < 0, as raízes complexas da equação quadrática ax2 + bx + c = 0 têm sempre a
forma:
Nesse
caso, dizemos que as soluções formam um par conjugado. A definição de conjugado complexo é dada no quadro abaixo.
Os
exemplos a seguir ilustram como obter os conjugados de números complexos na forma z = a + bi, em que a é a parte real e b a
parte imaginária.
Atividades:
1) Reescreva
as expressões abaixo usando a unidade imaginária i quando necessário.
2)
Resolva as equações abaixo.
a)
9x2 + 1 = 0
b)
25x2 + 16 = 0
c) x2
− 4x + 5 = 0
d) x2
+ 2x + 10 = 0
e) x2
− 12x + 40 = 0
f)
−x2 + 8x − 25 = 0
g) x2
− 5x + 7 = 0
h)
3x2 − 12x + 87 = 0
i)
4x2 + 4x + 5 = 0
j)
2x2 − 6x + 9 = 0
k)
4x2 + 24x + 85 = 0
l)
5x2 − 2x + 10 = 0
Teorema fundamental da álgebra
Já vimos que toda equação polinomial de grau n, com coeficientes reais, tem no máximo n raízes reais. Veremos agora que, trabalhando com números complexos, conseguimos resultados bem mais precisos, baseados no teorema abaixo, que apresentamos sem demonstração.
Observe
que o teorema fundamental da álgebra também se aplica a polinômios com
coeficientes reais, já que todo número real é também complexo.
Apresentado
dessa forma, o teorema parece pouco promissor, pois só indica que uma função
polinomial de grau n,
pn(x) = anxn
+ an−1xn−1 + an−2xn−2 + ⋯ + a1x + a0,
Entretanto, a sua combinação com o Teorema do Fator, nos permite decompor a função pn no produto de um fator linear por uma função polinomial pn−1, que tem grau n − 1:
Supondo,
então, que n − 1 seja maior que zero,
podemos aplicar novamente o teorema fundamental da álgebra, agora a pn−1.
Concluímos,
assim, que essa função também tem ao menos um zero complexo, e que é possível escrever:
e que é possível escrever:
Desse
modo,
em
que pn−2(x) é um polinômio
de grau n − 2.
Repetindo
esse processo outras n − 2 vezes,
chegamos à expressão
Esse
resultado é importante porque indica que é possível decompor uma função
polinomial de grau n em n fatores de grau 1, embora o teorema não explique como
os zeros de pn são
determinados.
Exemplo:
Já vimos que o polinômio p(x) = x4 − 4x3 + 13x2 podia ser escrito na forma p(x) = x2 (x2 − 4x + 13), bastando para isso que puséssemos x2 em evidência. Concluímos, assim, que x1 = 0 é uma raiz (de multiplicidade 2) de p(x) = 0.
Para
achar os outros zeros do polinômio, aplicamos a fórmula de Bhaskara à equação x2
− 4x + 13 = 0, calculando, em primeiro lugar, o discriminante:
∆ = (−4) 2 − 4 ⋅ 1 ⋅
13 = −36.
Uma
vez que já sabemos trabalhar com números complexos, não nos intimidamos com o
fato de o discriminante ser negativo, e prosseguimos escrevendo:
Assim,
as raízes (complexas) de
Finalmente,
lembrando que x1
= 0 também é um zero da função polinomial:
p(x) = x4 − 4x3 + 13x2
e
aplicando o Teorema da Decomposição, obtemos
p(x) = x2∙ (x − 2 − 3i)∙(x − 2 + 3i).
Observe
que, nesse exemplo, o coeficiente do monômio de maior grau do polinômio
original é a4 = 1.
Multiplicidade de zeros e pares conjugados
O
Teorema da Decomposição indica que é possível escrever uma função polinomial de
grau n como o produto de n fatores lineares que envolvem os zeros complexos da
função.
os zeros complexos da
função.
Entretanto,
não se exige que esses números sejam distintos. De fato, uma função quadrática
simples como p(x) = x2 − 10x +
25 pode ser apresentada na forma fatorada p(x) = (x − 5)∙(x
− 5), na qual o zero real x = 5
aparece duas vezes, tendo, portanto, multiplicidade
2.
Exemplo:
A
função polinomial
p(x) = 4x7 +44x6 +73x5
−508x4 −1070x3 +1400x2 −375x
pode
ser escrita na forma fatorada
p(x) = 4x∙(x
− 3)∙(x – 1/2 )2 ∙(x + 5)3.
Determine
os zeros da função e suas multiplicidades.
Solução:
Como já
dispomos da função na forma fatorada, concluímos trivialmente que seus zeros
são
x1
= 0, x2 = 3, x3 = 1/2 e x4 = −5.
A multiplicidade de cada zero c é o número
de vezes que o termo (x − c) aparece quando a função é apresentada na forma
fatorada.
Dito de outra forma, a multiplicidade de um
zero c é o expoente do fator (x − c).
Sendo assim, nesse problema,
• x1 = 0 tem multiplicidade 1,
• x2 = 3 tem multiplicidade 1,
• x3 = 1/2 tem multiplicidade 2,
• x4 = −5 tem multiplicidade.
No
problema acima, notamos que a soma das multiplicidades é exatamente igual ao
grau do polinômio. Esse resultado, que vale para toda função polinomial, está
resumido no quadro a seguir:
Exemplo:
Dada
a função p(x) = 5∙(x
+ 1)3∙(x
− 2 + i)2∙(x
− 2 − i)2, determine as raízes da equação p(x) = 0, bem como o grau de p.
Solução:
As raízes da equação p(x) = 0 são os zeros
da função, ou seja,
x = −1, x = 2 − i e x = 2 + i.
Já o grau de p pode ser obtido somando-se os
expoentes dos fatores lineares:
3 + 2 + 2 = 7.
Uma
função polinomial p tem como zeros x = 3 (com multiplicidade 2), x = 2i e x = −2i. Escreva a expressão de p, sabendo que p(0) = 144.
Solução:
Segundo o Teorema da Decomposição, a função
pode ser escrita na forma p(x) = a∙(x
− 3)2∙(x
− 2i)∙(x + 2i).
Sendo assim, temos
p(0) = a∙(0
− 3)2∙(0
− 2i)∙(0 + 2i). Substituindo x por
0.
p(0) = a∙(−3)2∙(−2i)∙(2i).
Simplificando os termos entre parênteses.
p(0) = a ⋅ 9 ⋅
(−4i2).
Calculando a potência e o produto.
p(0) = a ⋅ 9 ⋅
4. Usando o fato de que i2 = −1.
p(0) = 36a. Simplificando o resultado.
Como sabemos que p(0) = 144, concluímos que
36a = 144 ⇒ a = 144/36 = 4.
Logo, p(x) = 4∙(x
− 3)2∙(x
− 2i)∙(x + 2i).
Observe
que, nos exemplos anteriores, os zeros
complexos do polinômio apareceram em pares conjugados. No primeiro caso, esses
zeros eram 2 + 3i e 2 − 3i, enquanto no segundo tínhamos 2i e −2i.
De
fato, isso não ocorreu por acaso, mas como consequência direta de os
coeficientes do polinômio serem reais, como indicado no quadro abaixo.
Exemplo:
Escreva uma função polinomial de quarto grau,
com coeficientes reais, que tenha como zeros x1 = 1, x2
= −6, e x3 = 4 − 5i.
Como os coeficientes da função devem ser
reais, concluímos que os zeros complexos aparecerão em pares conjugados.
Assim, se x3 = 4−5i é um desses
zeros, devemos ter x4 = 4 + 5i.
Logo, a função terá a forma:
p(x) = a(x − 1)(x + 6)(x − 4 + 5i)(x − 4 −
5i).
Escolhendo a = 1 por simplicidade, obtemos
p(x) = (x − 1)(x + 6)(x − 4 + 5i)(x − 4 −
5i).
Atividades:
1) Determine
os zeros das funções polinomiais abaixo e indique suas multiplicidades. Informe
também o grau das funções.
a)
16(x − 2)2 (x + 7)3
b)
(x − 2 − 5i)(x − 2 + 5i)(x + 3 − 4i)(x + 3 + 4i)
c)
(x + 4)3 (x − 5 − 5i)(x − 5 + 5i)
d)
2(x − 1)(x − 1)(x − 1 − i)(x − 1 + i)
e)
(x − 8 − 2i)4 (x − 8 + 2i)4
f)
3x(x − 1 3 )(x − 3i)2 (x + 3i)2
2) Determine
as raízes das equações abaixo e escreva os polinômios do lado esquerdo na forma
fatorada.
a) 16x2 + 81 = 0
b) x3
− 9x = 0
c)
4x3 + 25x = 0
d) x3
+ 2x2 + 5x = 0
e)
2x3 − 16x2 + 50x = 0
f) x4
+ 4x2 = 0
g)
256x4 + x2 = 0
h) x5
+ 64x3 = 0
i) x4
+ 2x2 − 24 = 0
j) x4
+ 5x2 + 4 = 0
3) Determine
as raízes das equações abaixo e escreva os polinômios do lado esquerdo na forma
fatorada.
a) x3
+ 2x2 − 3x − 10 = 0, sabendo que 2 é raiz
b)
2x3 − 3x2 + 50x − 75 = 0, sabendo que 5i é raiz
c) x3
− 7x2 + 44x + 52 = 0, sabendo que 4 − 6i é raiz
d) x3
− 3x2 + 7x + 75 = 0, sabendo que −3 é raiz
e)
4x3 − 24x2 + 25x − 25 = 0, sabendo que 5 é raiz
4)
A decomposição de um polinômio p em
fatores do 1º grau é dada por: p(x) = 5
(x + 1) (x – 3) (x – 4).
As
raízes desse polinômio são:
(A) 5, 3 e 4
(B) −1, 3 e 4
(C) 1, −3 e −4
(D) 5, −3 e −4
Gráficos
nas funções polinomiais de graus diversos
De
forma geral, o gráfico de uma função polinomial possui as seguintes
características:
1)
Ele é contínuo, ou seja, ele não
contem buracos, saltos (descontinuidades verticais) ou falhas (descontinuidades
horizontais), como o que se vê nas Figuras 2)(a) e 2)(b).
2)
Ele é suave, ou seja, ele não possui
mudanças bruscas de direção ou inclinação, como as mostradas na Figura 2)(c).
Essas mudanças são denominadas informalmente de quinas ou bicos.
(a)
Não é o gráfico de uma função polinomial, pois há um buraco em a e um salto em b.
(b)
Não é o gráfico de uma função polinomial, pois há uma falha entre a e b.
(c)
Não é o gráfico de uma função polinomial, pois há uma quina em a e um bico em b.
(d)
Pode ser o gráfico de uma função polinomial, pois é contínuo e suave.
Otimização do formato de uma caixa
Uma
folha de papelão com 56 × 32 cm será usada para fabricar uma caixa sem tampa,
como a que é mostrada na Figura abaixo:
Para
obter a caixa, a folha de papelão deverá ser cortada nas linhas contínuas e
dobrada nas linhas tracejadas indicadas na Figura abaixo:
Observe que a base da caixa corresponde ao retângulo interno da Figura acima e que a altura da caixa é x.
Responda
às perguntas abaixo, lembrando que o volume de um prisma retangular de lados x, y
e z é igual a xyz.
a)
Exprima em função da variável x cada
uma das duas dimensões do fundo da caixa dobrada.
b)
Determine uma função V(x) que forneça
o volume da caixa em relação a x.
c)
Defina um domínio adequado para V,
considerando que os lados da caixa não podem ser negativos.
d)
Esboce o gráfico de V(x).
e) A
partir do gráfico de V(x), determine
o valor de x que maximiza o volume da
caixa. Calcule o volume correspondente.
Solução:
a) Observando a Figura, notamos que a folha
de papelão tem 56 cm de largura. Desse comprimento, uma parcela correspondente
a 4x deve ser reservada para formar a lateral da caixa. Assim, a largura do
fundo da caixa é dada por L(x) = 56 − 4x.
Por sua vez, dos 32 cm de altura que a folha
de papelão possui, 2x devem ser usados na lateral da caixa, de modo que a outra
dimensão do fundo da caixa é definida por A(x) = 32 − 2x.
b) Dadas as dimensões do fundo da caixa, e
considerando que sua altura mede x, o volume comportado será equivalente a V
(x) = (56 − 4x)∙(32
− 2x)∙x.
c) Como nenhuma dimensão da caixa pode ser
negativa, devemos impor as seguintes condições:
a) x ≥ 0.
b) 56 − 4x ≥ 0, o que nos leva a x ≤ 14.
c) 32 − 2x ≥ 0, que implica que x ≤ 16.
Tomando a interseção dessas desigualdades,
obtemos
D = {x ∈ R ∣
0 ≤ x ≤ 14}.
d) Claramente, a função V(x) tem como zeros
x = 0, x = 14 e x =
16.
Entretanto, como vimos no item anterior,
somente os valores de x entre 0 e 14 têm sentido físico.
Limitando nosso gráfico a esse intervalo,
obtemos a curva mostrada no gráfico abaixo:
e)
Analisando a Figura do item d, concluímos que a altura que maximiza o volume da
caixa é x ≈ 5cm, à qual corresponde um volume aproximado de
V(5) = (56 − 4 ⋅
5)(32 − 2 ⋅ 5) ⋅ 5 = 3960 cm3
Atividades:
1) Dados os gráficos abaixo, determine quais podem
representar uma função polinomial. Caso o gráfico não possa corresponder a uma
função polinomial, indique o motivo.
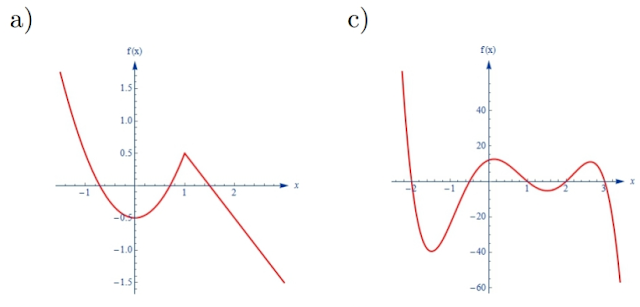
2) Considerando apenas o comportamento extremo das funções abaixo, relacione-as aos gráficos apresentados.
a) f(x) = x3 − 5x + 1
b) f(x) = −2x3 − x2 + 4x + 6
c) f(x) = x4 − 3x3 − 2x2 + 4x – 4
d) f(x) = 1 − 4x2 − 4x3 + 3x4 + 2x5
− x6
3)
Os gráficos de algumas funções polinomiais foram desenhados abaixo, com o
auxílio de um programa matemático. Determine aproximadamente os pontos de
mínimo e máximo local e os valores correspondentes de cada função.
4) Uma companhia aérea permite que um passageiro leve consigo uma
bagagem cuja soma das dimensões (altura, largura e profundidade) não ultrapasse
150 cm. Joaquim pretende tomar um voo dessa companhia levando uma caixa cuja
base é quadrada. Suponha que o comprimento do lado da base seja x.
a)
Escreva uma função h(x) que forneça a
altura da caixa em relação às outras duas dimensões.
b)
Forneça uma função V(x) que forneça o
volume da caixa, lembrando que o volume de um prisma retangular de lados x, y
e z é igual a xyz.
c)
Defina um domínio adequado para V(x),
lembrando que nenhum lado da caixa pode ter comprimento negativo.
d)
Esboce o gráfico de V(x) no domínio
que você escolheu.
e)
Determine o valor de x que maximiza o
volume da caixa. Calcule o volume correspondente.
5) Um caixa sem tampa é feita a partir de um pedaço de cartolina de 60cm
de lado, cortando-se quadrados iguais de cada canto e dobrando-se os lados.
a) Qual a função V(x) em
relação ao volume da caixa?
b) Cortando-se quadrados de lado 10 cm nos cantos e dobrando
conforme a figura, é possível formar uma caixa sem tampa cujo volume é igual a
16.000 cm3. Verifique se existe outra medida que pode ser cortado os
quadrados para que o volume seja também 16.000 cm3.
6) Deseja-se
cortar quadrados em cada canto de uma folha de papelão quadrada, com 18 cm de
lado para obter uma caixa de papelão na forma de um paralelepípedo sem tampa.
a)
Determine o polinômio que representa o volume da caixa em relação ao lado de
medida x dos quadrados cortados.
b)
Cortando-se quadrados de lado 4 cm nos cantos da folha é possível construir uma
caixa de 400cm3. Existe algum outro valor para o lado do quadrado a
ser recortado em cada canto para qual o volume da caixa resultante também seja
igual a 400cm3? (Utilize a calculadora para calcular a raiz não
exata)
7) Um
quadrado de papelão tem 20 cm de lado. Cortando quadradinhos iguais, nos quatro
cantos, podemos montar uma caixa em forma de bloco retangular.
a)
Determine a função V(x) referente ao
volume da caixa.
b)
Sabendo-se que se cortar quadrados de 5 cm obteremos um volume de 500 cm3.
É possível obtermos outros valores referentes à medida que deve ser cortado os
quadrados para obter o volume de 500 cm3?
8)
Um quadrado de cartolina em forma de bloco retangular, vamos cortar os cantos
da cartolina, retirando quadradinhos em x
cm. Quais devem ser os valores de x,
em centímetros, para que a capacidade seja de 72 ml?
9)
Para fazer uma caixa, foi utilizado um quadrado de papelão de espessura
desprezível e 8 dm de lado, do qual foram recortados e retirados seis quadrados
menores de lados x. Em seguida, o
papelão foi dobrado nas linhas pontilhadas, assumindo a forma de um
paralelepípedo retângulo, de altura x, como mostram os esquemas ao lado. Quando
x = 2 dm, o volume da caixa é igual a
8 dm³. Determine outro valor de x para que a caixa tenha volume igual a 8 dm³.
10) (ENEM-2009) Muitas
indústrias têm procurado modificar as embalagens de seus produtos de forma a
economizar material, mas mantendo o mesmo volume. Considere que se tenha uma
folha de papelão quadrada e se deseje encontrar a melhor altura (h) para fazer
uma caixa sem tampa, cortando-se os quatro cantos da folha. As exigências são
que as dimensões da caixa sejam números inteiros e que o volume seja o maior
possível. No modelo apresentado na figura seguinte, a folha tem 12 cm de lado
e, nesse caso, a caixa de maior volume terá altura 2 cm. Para encontrar esse
número, é calculado o volume em função da altura e prossegue-se atribuindo
valores a h e calculando o volume, enquanto o valor do volume aumentar.
(A) 2 cm
(B) 3 cm
(C) 4 cm
(D) 5 cm
(E) 6 cm
11) Qual o possível polinômio
do P que se refere ao gráfico abaixo?
12) Um ciclista e um corredor começam, juntos, uma competição. A curva abaixo, cuja equação é dada por e = t3 + at2 + bt + c, representa a posição e, em metros, o ciclista, em função do tempo t, em segundos, em que a, b e c são números reais fixos.
a) A partir do gráfico a cima,
encontre os valores de a, b e c
fixos e a escreva a função com esses devidos valores.
b) No instante em que o ciclista parte da posição zero, o corredor inicia um movimento, descrito pela equação e = 4t, na mesma pista e no mesmo sentido. Determine a posição mais afastada da origem na qual o ciclista e o corredor voltam a se encontrar.
13) Os gráficos de duas
funções polinomiais P e Q estão representados na figura seguinte.
Para que valores
de x, temos P(x) = Q(x)?
14) Angelo e Benito participaram de uma corrida de 800 metros. O gráfico abaixo mostra a distância percorrida, em função do tempo, para os dois corredores, sendo que Benito chegou à frente de Angelo.
Quanto tempo decorreu entre as chegadas de Benito e Angelo?



















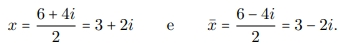


































Nenhum comentário:
Postar um comentário