Pitágoras nasceu na ilha grega de Samos. Viajou muito antes de se estabelecer em Crotona, sul da Itália. Aí, Pitágoras fundou a escola pitagórica, onde se estudavam Matemática, Música, Astronomia e Filosofia. Muitas descobertas são atribuídas aos membros dessa escola, como por exemplo a de que a Terra tinha a forma esférica.
Na
Matemática, o grande feito dos pitagóricos foi demonstrar que:
Em todo triângulo retângulo, o
quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos
catetos.
Este
teorema é chamado, até hoje, teorema de Pitágoras, embora muito antes, já fosse
conhecido pelos babilônios.
Utilizando o Teorema de Pitágoras,
calcular a medida da diagonal do retângulo de medidas: 3 e 4.
d2 = 32 + 42
d2 = 9 + 16
d2 = 25
d = √25
d = 5
Os antigos egípcios usavam um método, no
mínimo curioso, para medir e demarcar suas terras. Utilizavam uma corda com
treze nós distribuídos em intervalos iguais:
Essa corda era fixada ao chão através de
três estacas colocadas em pontos estratégicos. Veja a figura:
Se a corda ficasse bem esticada, o ângulo
formado pela estaca era reto.
Enquanto os egípcios faziam e desfaziam nós, os hindus iam um pouco mais além. Eles sabiam, por exemplo, que triângulos com lados medindo 6, 8 e 10; 9, 12 e 15; 12, 16 e 20; 15, 20 e 25, eram todos triângulos retângulos, pois possuem medidas que são múltiplos do triângulo de medida 3, 4 e 5, feito no exemplo acima.
Mas, coube a Pitágoras e seus discípulos, a primeira demonstração da relação existente entre os lados de um triângulo retângulo.
Calcular a medida da hipotenusa do
triângulo retângulo de catetos de medidas 1 e 3.
d2 = 12 + 32
d2 = 1 + 9
d2 = 10
d = √10
Um número real entre os inteiros 3 e 4,
mais próximo de 3, na reta numérica real, por exemplo.
Atividades:
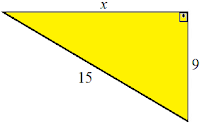
1) Determine x em cada triângulo retângulo abaixo:
a)
b)
c)
2) Verifique se o triângulo de medidas
abaixo é retângulo:
a) 8, 15 e 17.
b) 1, √2 e √3
3) (ENEM) O topo de uma escada de 25 m de
comprimento está encostado na parede vertical de um edifício. O pé da escada
está 7 m de distancia da base do edifício, se o topo escorregar 4 m para baixo
ao longo da parede, qual será o deslocamento do pé da escada?
|
(A) 4 m (B) 8 m (C) 9 m (D) 13m |
6) Entre que números inteiros está a medida da diagonal de um retângulo de medidas 4 e 6.
7) Aparelhos de TV e monitores
de computador são vendidos com medidas em polegadas. Para se saber quantas
polegadas possui a tela de uma televisão, basta medir na diagonal, de um canto
a outro da tela. Carla mediu o comprimento e a largura da tela de sua televisão
e encontrou as medidas indicadas na figura abaixo.
A
televisão de Carla é de quantas polegadas?
(A) 12.
(B) 16. (C) 20. (D) 28.
8) Uma certa quadra de poliesportiva possui 16
metros de largura e diagonal medindo 34 metros. Determine área dessa quadra?
9) Calcular o valor de x no triângulo retângulo:
10) Calcular o valor da x na figura abaixo:
11)
A figura, abaixo, representa a planta de uma praça triangular. Ela é contornada
por uma calçada e há um atalho, representado na figura pelo caminho RQ,
perpendicular a um dos lados.
Para ir do ponto M ao ponto P,
Júlia percorreu o trecho MQRP, andando sempre sobre a calçada. Qual foi a
distância percorrida por Júlia?
(A) 35 m.
(B) 48 m.
(C) 52 m.
(D) 72 m.
12) Em um triângulo retângulo,
a hipotenusa mede 25 cm e a soma dos catetos é 35 cm. Determine a medida de
cada cateto.
13) Os catetos de um triângulo
retângulo têm a mesma medida. Se a hipotenusa mede
14) Marque no
plano cartesiano as coordenadas dos vértices nomeie o tipo de figura geométrica
que aparece:
a) A(3, 4),
B(5, 3), C(3, 2) e D(1, 3)
b) A(3, 4),
B(1, 4) e C(2, 1)
15) Determine a distância entre os
pontos:
a) A(3, 2) e
B(3, 5).
b) C(4, 3) e
D(7, 3).
c) E(2, 3) e F(6,6).
d) G(–2, 2) e H(4, 8).
e) M(–4, –4) e N(4, 4).
f) P(−5, −6) e Q(−3, −8).
g) R(−6,8) e S(−3,9).
16) Uma pessoa percorres 7 km
na direção norte; depois, 8km na direção leste; finalmente 1 km n direção sul.
Calcule a distância entre os pontos inicial e de chegada.
17) Um homem percorre, em
sequência, 10 km na direção leste, 3 km na direção sul, 5 km na direção leste e
11 km na direção norte. Calcule a distância entre os pontos de partida e de
chegada.
18) O perímetro de um
retângulo é
19) Um retângulo tem área
igual a 6
cm2. Como um de seus lados mede 3 cm, calcule a diagonal desse
retângulo.
20) Antigo Problema Chinês:
Estre problema consta do livro
Lilavati, escrito pelo matemático
hindu Bhaskara (século XII). Se um
bambu de 32 cúbitos de altura é quebrado pelo vento, de modo que a ponta
encontre o chão a 16 cúbitos da base, a que altura (em cúbitos) a partir do
chão?
(Cúbito ou côvado – antiga unidade de medida de comprimento equivalente a três
palmos ou 66 cm)
21) Um bambu de 3 m de altura
é dobrado em dois pedaços pelo vento. O pedaço inferior permanece em pé,
perpendicularmente em relação ao solo, enquanto o superior tomba de modo que
sua extremidade encontra o chão a 1,2 m da base do bambu. Faça um desenho
representando a situação e determine a que altura do chão encontra-se a
rachadura.
22) Um cabo liga dois edifícios próximos, como se vê na figura a seguir:
Use os dados indicados na
figura para determinar o comprimento do cabo entre os pontos A e B.
23) Na figura abaixo, representa o projeto de uma escada com 5 degraus de mesma altura:
O comprimento do corrimão é igual a:
(A) 1,8 m.
(B) 1,9 m.
(C) 2,1 m.
(D) 2,2 m.
24) Calcule as medidas
desconhecidas a, b, c, d, e:
Aplicações do Teorema de Pitágoras
Diagonal do quadrado:
1) Calcular a medida da diagonal do
quadrado de 4 cm de lado:
Cada um dos dois triângulos é
retângulo. Aplicando, em um deles, o teorema de Pitágoras, temos:
d2 = 42 + 42
d2 = 2 x 42
d = 4 √2
2) Calcular a medida da diagonal do
quadrado de medida a qualquer:
d2 = a2 + a2
d2 = 2 x 42
d = a √2
Como consequência do teorema de Pitágoras, a medida da diagonal d de um quadrado de lado l pode ser expresso pela fórmula:
Atividades:
1) Calcular o valor da diagonal das
figuras abaixo:
2) O perímetro de um quadrado é
3) Um quadrado tem área igual
a 25 cm2. Qual a medida da diagonal desse quadrado?
4) A diagonal de um quadrado tem 7√2 cm. Determine o perímetro e a área do quadrado.
5) Um terreno tem formato quadrado e a medida de sua
diagonal é de 24 centímetros. Determine a medida de seus lados.
6) Quanto Eliza caminha de
um canto de uma praça quadrada até outro, fazendo uma diagonal, sabendo que cada lado da
praça mede 50 metros. (Use √2
7)
Uma praça quadrada é cortada na diagonal por um calçadão. Para ir de um extremo
ao outro dessa diagonal, quem anda mais: uma pessoa que utiliza o calçadão ou
uma pessoa, que contorna a praça? (Use
1) Calcular a medida do triângulo isósceles abaixo:
O triângulo isósceles
possui dois lados com mesma medida, o terceiro lado é cortado pela altura h do
triângulo, se for identificado como base do triângulo isósceles, no seu ponto
médio, dividindo essa medida da base em duas partes iguais.
Desse modo, temos dois
triângulos retângulos com medidas de lados iguais. Separando um triângulo
retângulo, podemos utilizar o teorema de Pitágoras, da seguinte maneira:
h2 + 62
= 102
h2 + 36 = 100
h2 = 100 – 36
h2 = 64
h = √64
h = 8.
Atividades:
1) Calcular a medida da altura dos
triângulos abaixo:
2) Calcule o valor das medidas x indicadas:
a)
b)
c)
d)
3) Calcule a altura e a área de um triângulo
isósceles, sabendo que os lados congruentes medem
4)
Em um triângulo isósceles, 16 cm é a medida relativa à base, que mede 24 cm.
Calcule o perímetro desse triângulo.
Altura do Triângulo Equilátero:
1) Calcular a altura e a área do triângulo equilátero abaixo:
Como todo triângulo equilátero é também
isósceles, o lado da base é dividido em duas partes de mesma medida pela
altura, então, utilizando o teorema de Pitágoras no triângulo retângulo formado
pela altura, temos:
h2 + 22
= 42
h2 + 4 = 16
h2 = 16 – 4
h2 = 12
A área do triângulo é dada por:
2)
Calcular a altura e a área de um triângulo de equilátero de medida a qualquer:
Pelo teorema de Pitágoras, temos:
A área do triângulo é dada por:
Como consequência do teorema de Pitágoras, a medida da altura h de
um triângulo equilátero de lado l pode ser expresso pela
fórmula:
E sua área
A é dada pela fórmula:
Atividades:
1) Calcule a altura e área de
um triângulo equilátero cujo lado mede 6 cm.
2) O perímetro de um triângulo
equilátero é
3) A altura de um triângulo equilátero mede 5√3 cm. Calcule a área desse triângulo.
4) Em um triângulo equilátero,
qual a medida da altura, se o lado mede 8 cm ?
5) Em um triângulo equilátero,
qual a medida da área, se a altura mede 12 cm ?
Medidas laterais e altura de um Trapézio:
1) Em um trapézio isósceles a
base maior é igual a 14 cm e base menor é igual a 8 cm e os lados oblíquos
medem 5 cm. Determine a altura deste trapézio e sua área.
Na
figura acima, é possível notar que a altura do trapézio é dada pela variável h, e a base maior pode ser dividida em
três medidas diferentes, subtraindo 14 por 8 e resultado dessa subtração, divide
por dois, obtendo as duas outras medidas.
Como
foi obtido um triângulo retângulo com o lado oblíquo do trapézio, com a altura h e a medida 3 da parte da base maior,
podemos utilizar o teorema de Pitágoras da seguinte forma:
h2 + 32
= 52
h2 + 9 = 25
h2 = 25 – 9
h2 = 16
h = √16
h = 4
Logo,
a altura desse trapézio é 4 cm.
A
área será dada por:
(14 + 8) x 4 / 2 = 22 x 2 = 44 cm2.
Atividades:
1) Um trapézio retângulo de
2) As bases de um trapézio
isósceles medem
3) Em um trapézio isósceles, a
base menor mede 8 cm, um lado oblíquo vale 13 cm e 12 cm é a medida da altura.
Calcule a medida da base maior.
4) Em um trapézio retângulo, a
base menor, a altura e o lado oblíquo medem, respectivamente, 6 cm, 5 cm e 13
cm. Calcule a medida da base maior.
5) No trapézio representado pela figura abaixo, a sua área é dada por 24 cm2. Sabendo que sua base maior mede 8 cm e uma de suas partes que foi dividida pela altura é 3 cm, determine os valores das medidas x e y desconhecidas:
6) Numa casa de espetáculos
com a forma de um trapézio, conforme a figura abaixo, deseja-se colocar uma
suporte de canhão de iluminação de uma ponta a outra do teatro de forma
diagonal, conforme o pontilhado da figura. Com as dimensões da casa conhecida, com
que medida que deve ser comprado o suporte?
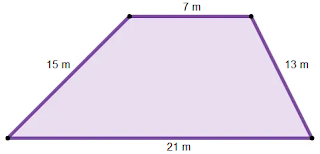
7) A figura abaixo representa
um terreno de uma praça cuja forma é um trapézio escaleno com as dimensões
indicadas em metros.
A prefeitura pretende fazer um
projeto, que possui os custos:
a) Para colocar uma grade
cobrindo toda a praça, deve gastar 10 reais por metros.
b) colocar um calçamento na
praça, que custa 40 reais por metro quadrado.
Qual o valor total que a
prefeitura deve gastar com esse projeto?
Medidas de diagonais de um Losango:
1) Num losango, as diagonais medem 16 cm e 12 cm. Determine a medida do lado do losango.
2) As diagonais de um losango medem 18 cm e 24 cm. Calcule a medida do lado desse losango.
3) As diagonais de um losango medem 6 cm e 8 cm. Qual o perímetro desse losango?
O que são números pitagóricos ?
Os números inteiros
positivos, que arrumados de três em três, são chamados de pitagóricos quando satisfazem o teorema de
Pitágoras.
Exemplos:
|
3 |
4 |
5 |
32 + 42
= 52 |
9 + 16 = 25 |
|
5 |
12 |
13 |
52 + 122
= 132 |
25 + 144 = 169 |
|
7 |
24 |
25 |
72 + 242
= 252 |
49 + 576 = 625 |
|
9 |
40 |
41 |
92 + 402
= 412 |
81 + 1.600 = 1.681 |
Apesar de os babilônios já conhecerem esses números mil anos antes de Pitágoras, este último que levou a fama.
São conhecidas algumas fórmulas que
fornecem números pitagóricos:
a)
a
= 2k2 + 2k + 1
b
= 2k + 1
c
= 2k2 + 2k,
onde k é inteiro positivo, atribuídos a Pitágoras;
b)
a
= p2 + q2
b
= 2pq
c
= p2 – q2 (p > q),
onde p e q são números
inteiros positivos, atribuídos a Platão.
Outras ternas pitagóricas: (20, 21, 29); (11, 60, 61); (8, 15, 17); (12, 35, 37); (16, 63, 65); (20, 99, 101).
Atividade:
Os três lados de um triângulo retângulo são números inteiros. Um dos catetos mede 17. Qual é o perímetro desse triângulo?





























































Nenhum comentário:
Postar um comentário