1) Números Quadrados Perfeitos:
Se nós quisermos encontrar o comprimento de um quadrado que possui área igual a 16, a resposta deverá ser 4, pois
4 x 4 = 42 = 16.
A raiz quadrada é a operação inversa de um número elevado ao quadrado e será representada pelo símbolo √. No caso do exemplo anterior, dizemos que √16 = 4 ("raiz quadrada de 16 é 4"). Esse símbolo para raiz quadrada é empregado desde os anos 1500.
Vejamos algumas raízes
quadradas que se originam de números inteiros:
Todos os números quadrados perfeitos possuem números inteiros como raízes
quadradas.
Existe outra notação para as raízes
quadradas. Do mesmo modo que x2 de nota um número quadrado, pode se
escrever a raiz quadrada de um número como x1/2, que se enquadra no
dispositivo de se multiplicar números somando suas potências.
2) Como calcular as raízes quadradas:
?Há, no entanto, diversas falhas ao longo da reta numérica entre esses quadrados perfeitos.
Essas falhas são 2, 3, 5, 6, 7, 8, 10,
11... Todos esses números têm raízes quadradas, mas essas raízes não são iguais
a números inteiros.
Praticamente todas as calculadoras têm
uma tecla √ e usando-a encontramos, por exemplo, que
√7 =
2,645751311064591..., ou seja é possível dizer que (2,645751311064591...)2
= 7.
3)
O que são números irracionais?
O mesmo ocorrerá com
que se forem verificadas na calculadora
não chegaremos a uma representação decimal exata nem a uma dízima periódica.
Portanto, não são números racionais, serão o que chamamos de números irracionais.
Por muito tempo, acreditou-se que os números racionais eram suficientes para medir todos os segmentos de reta, ou seja, todos os segmentos de reta era comensuráveis.
4)
Como surgiram os números irracionais?
Os discípulos de Pitágoras também acreditavam nisso, porém desde o século V a.C. desconfiavam da existência de números irracionais que representariam segmentos de reta incomensuráveis. Pois nessa época, eles estavam empenhados em determinar a medida da diagonal de um quadrado, e se depararam com um problema aparentemente insolúvel.
Para determinar a medida da diagonal de
um quadrado, cujos lados mediam uma unidade de comprimento, aplicavam o teorema
que leva até hoje o nome de Pitágoras:
“Em todo triângulo retângulo, a medida da hipotenusa ao quadrado é igual à soma dos quadrados das medidas dos catetos.”
5)
Teorema de Pitágoras:
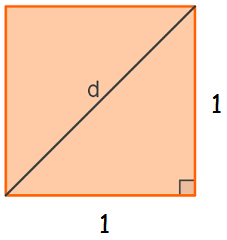
Tomando o quadrado de medida 1, é
possível notar que sua diagonal divide-o em dois triângulo retângulos
congruentes, cujos catetos medem 1, e a diagonal procurada (d) é a hipotenusa dos triângulos
retângulos:
Desse
modo, pelo Teorema de Pitágoras temos:
d2
= 12 + 12
d2
= 1 + 1
d2
= 2
Mas,
qual o número real positivo cujo quadrado é igual a 2 ?
Pitágoras e seus discípulos conseguiram observar que:
1,42
= 1,96 e 1,52 = 2,25; logo o número procurado está entre 1,4 e 1,5.
Depois,
notaram que 1,412 = 1,9881 e 1,422 = 2,0164; logo o
número procurado está entre 1,41 e 1,42.
Continuando
esse processo, exaustivo, perceberam que nunca iriam encontrar um número
racional positivo cujo quadrado fosse exatamente igual a 2.
Por isso, que é considerado que assim surgiram os números irracionais. Por exemplo:
representa o número irracional cujo quadrado é igual a 2.
Vejamos, agora, utilizando o Teorema de Pitágoras, como calcular a medida da diagonal do quadrado de lado 2:
d2
= 22 + 22
d2
= 4 + 4
d2
= 8
Logo, a medida que representa a diagonal desse quadrado é √8, um número irracional cujo quadrado é igual a 8.
6) Ordem
nos Números Irracionais
Identifique o padrão:
Verifica-se que:
Pergunta para reflexão
Quando você eleva ao quadrado a
raiz quadrada de um número...
( ) a resposta é menor que o
número original.
( ) a resposta é o número
original.
( ) a resposta é maior que o
número original.
Sem usar calculadora, vamos organizar
os seguintes números em ordem crescente.
Etapa 1: Eleve todos os números ao quadrado:
Etapa 2: Ordene os números em ordem crescente:
A
Resposta:
Pergunta para reflexão
Para ordenar raízes quadras e
inteiros, qual das estratégias a seguir é melhor?
Por exemplo:
( ) Eleve ao quadrado apenas as raízes ao quadrado. Por exemplo:
( ) Eleve ambos ao
quadrado, as raízes quadradas e os inteiros. Por exemplo:
7) Operações com radicais:
Observe que a equação d2 = 4 + 4, pode ser resolvida de outra forma, da
seguinte maneira:
Essa maneira de escrever 2
Observe que um radical elevado ao
quadrado é igual ao próprio número do radicando, como:
pois são operações inversas, daí é possível perceber que também:
De modo geral, temos algumas propriedade
de radicais, aplicadas aqui:
Exemplo: Calcular as operações com números irracionais abaixo:
a) 
Segue a propriedade f), nada a ser feito,
ficará desta forma como linguagem de radical, um número irracional, que é soma
de um irracional com um racional.
b)
Segue a propriedade f), nada a ser feito,
ficará desta forma como linguagem de radical, um número irracional, que é soma
de um irracional com um irracional.
c) 
Basta reduzir a linguagem de radical,
excluindo o sinal de multiplicação, da seguinte forma:
d) 
Segue a propriedade b):
e) 
Segue a propriedade b):
Ou segue a propriedade a):
g) 
Segue a propriedade c)
1)
Entre que números inteiros encontra-se
?
2) Entre os números reais 
a) quantos números naturais existem? E
números inteiros?
b) quantos números racionais existem? E
números irracionais?
3) Calcule as operações com
números irracionais abaixo:
4) Calcule a medida x das
figuras abaixo:
a)
b)
5) Calcule a área das
figuras abaixo:
a)
b)
d)
e)
6) Calcule o valor da
expressão 
.
7) Na reta numérica real,
determine a distância entre 
8) Vamos
relembrar: 
Use essa ideia e
escreva de forma simplificada:
9) Analise cada expressão e corrija se necessário:
10) Para a = 64, ache mensalmente o valor destas
expressões:
11) Quando p = 3 e q = 4, ache os valores de:
12) Quanto vale 
?
13) Qual o valor
aproximado de
, utilizando a aproximação de 
?
14) O
número 
está
situado entre que números inteiros?
15) Encontre um número real entre –3 e
–5/2.
16) Encontre um número real y que satisfaça a seguinte
desigualdade:
< y <
2.
17) Identifique em cada número abaixo se é racional ou irracional:
b) 0,77 ___________________________________
c) 0,77555... _______________________________
d) 0,71727374... ____________________________
18) Dê exemplos de:
a) dois números irracionais cuja soma é irracional.
b) dois números irracionais cuja soma é racional.
c) dois números irracionais cujo produto é irracional.
d) dois números irracionais cujo produto é racional.
19) Dado o conjunto
, determine:
a) O menor número do conjunto A:
_____________________________________
b) O maior número do conjunto A:
_____________________________________
c) Coloque na ordem crescente
_____________________________________
d) Quais desses números são racionais?
_____________________________________
20) Complete as lacunas com maior (>) ou menor (<):
b) 4,132 _____ 4,222
c) 1,5 _____ 1,555...
d) 2 ____ 
21) Suponha que x
e y sejam dois números racionais. Em
cada caso, diga se o número indicado é racional ou irracional, ou pode ser
racional ou irracional:
a) x + y
b) x – y
c) x ∙ y
d) x / y
e) √x
f) x + √2
22) Suponha que x
e y sejam dois números irracionais.
Em cada caso, diga se o número indicado é racional ou irracional, ou pode ser
racional ou irracional:
a) x + y
b) x – y
c) x ∙ y
d) x / y
e) √x
f) x + √2
23) Calcule o valor das expressões:
a) (–1)2 – 11·(–1) + 28 =
b) (–11)2 – 11
x (–11) =
24) Na casa
de João existe um quarto cujo chão é quadrado e tem 16 m2 de área.
Quanto mede o lado desse quadrado?
O número π (“pi”)
Supondo que a
Terra seja esfera com raio 6.400 km, qual é o comprimento da linha do equador?
O comprimento de
uma circunferência é dado pela fórmula
C = 2πR,
onde R é a medida do raio da circunferência e
π é um número irracional.
Assim, a linha do
equador mede, aproximadamente,
C ≈ 2 x 3,14 x 6.400, isto é,
C ≈ 40.192 km.
Para efetuarmos
esses cálculos usamos um número irracional chamado “pi” e representa pela letra grega π.
Como surgiu o número π ?
Há mais de
quarenta séculos, já era conhecido o fato de que dividindo-se o comprimento C de uma circunferência pela medida do
seu diâmetro d (tomamos numa mesma
unidade de comprimento), o resultado obtido era sempre o mesmo, qualquer que
fosse a circunferência.
Os antigos
egípcios utilizavam C/d = 3,16; os babilônios, 3,12.
Arquimedes,
matemático e físico grego do século III a.C., 22/7.
Ptolomeu,
matemático e astrônomo grego do século II d.C., 3,1416.
O valor de
Em 1430, o
matemático árabe Al Kashi conseguiu uma aproximação do π com dezesseis casas decimais.
Em 1706, Williams
Jones, matemático inglês, passou a indicar o valor exato do “pi” pela letra π, inicial da palavra grega periferia:
περεϕερεια
Mais tarde, em
1761, o matemático suíço J. H. Lambert prova que, em notação decimal, o π tem infinitas casas decimais que não
formam período, sendo, portanto, um número irracional.
Hoje, graças a
possantes computadores, conhecemos o valor de π com trilhões de casas decimais.
1) Calcular o
valor das expressões:
a) (π – 3) + (π +
5) =
b) (π – 3) – (π +
5) =
c) (π – 3) ∙ (π +
5) =
d) √π ∙ √2 =
2) O raio de uma
bicicleta de aro 26 mede 30cm. Qual é o comprimento da roda de uma bicicleta
aro 26? Qual a distância que essa roda percorre em uma volta?
3) O diâmetro dos
pneus das rodas de um carro mede, aproximadamente, 50 centímetros. O número de
voltas dadas pelas rodas desse carro, ao percorrer uma estrada de 300 km, está
próximo de:
(A) 2.000 voltas.
(B) 20.000 voltas.
(C) 200.000 voltas.
(D) 2.000.000 voltas.
A Razão Áurea
O número de outro (ou
razão áurea) é uma famosa constante matemática representada pela letra grega φ (fi
maiúsculo), cujo valor exato é 
Sua fama
se dá devido a diversos contextos naturais onde aparece. Por exemplo, se
dividirmos o comprimento de cada falange (ossos que formam os dedos) pelo
comprimento da falange menor ligada a ela, obteremos, para a maior parte dos
seres humanos, um valor bastante próximo de φ.
Justamente
por essa ocorrência natural, muitos artistas consideram que a razão áurea é
naturalmente agradável aos olhos e tentam reproduzi-la em suas obras. No
Partenon, templo dedicado à deusa grega Atena, construído há mais de 1.500
anos, a razão áurea aparece em várias ocasiões. Uma delas é a própria fachada:
se dividirmos a largura da construção por sua altura obteremos um valor próximo
a φ.
O retângulo
cuja razão entre os lados é igual a φ é denominado retângulo áureo.
Um
conceito intimamente ligado ao número áureo é a sequência de Fibonacci, cujos
dois primeiros termos são iguais a 1 e cujos termos a partir do terceiro são
iguais à soma dos dois termos anteriores: (1, 1, 2, 3, 5, 8, ...).
Essa
sequência é tal que, escolhido um termo qualquer a partir do segundo, o
quociente entre esse termo e seu antecessor é tão mais próximo de φ quanto
maior for o termo escolhido.
1) Pedro
quer construir uma mesa cujo tampo tenha a forma de um retângulo áureo. Se um
dos lados desse retângulo tiver 1 m, qual das alternativas apresenta uma medida
possível para o outro lado?
(A) 6,18 m
(B) 0,618 m
(C) 0,162 m
(D) 1,68 m
2) Ao
chegar à loja, Pedro constatou que comprar o tampo retangular num formato
pré-fabricado seria muito mais barato. As opções disponíveis na loja eram as
seguintes:
I) 2 m x 1 m
II) 130 cm x 80 cm
III) 110 cm x 68 cm
Qual ou quais dessas opções apresentam
formato mais próximo do retângulo áureo?
 |
| Catedral de Notre Dame (Paris) |
Arquitetos
e pintores de várias gerações têm considerado o retângulo áureo uma das formas
cujas dimensões apresentam uma relação perfeita e harmoniosa. Além de ser
utilizado pelos gregos em sua arquitetura, muitas obras clássicas do Renascimento,
como Mona Lisa, do italiano Leonardo da Vinci (1452-1519).
Os
padrões áureos facilmente podem ser encontrados na natureza, formando padrões
expressamente harmônicos. Manifestam-se no crescimento das plantas, nos
insetos, nos animais, nas proporções do corpo humano.
Um dos primeiros estudiosos sobre as proporções humanas foi Marcus Vitruvius Pollio, arquiteto e escritor romano do século I. Esse estudioso alegava que um corpo bem formado devia apresentar proporções harmoniosas.
Observe a
interpretação que Leonardo da Vinci fez das ideias de Vitruvius, quase quinze séculos
mais tarde.
Na prática, usamos 1,61803 ou ainda 1,6 como valor aproximado de ϕ, mas já vimos que ϕ não é racional.
Compare algumas razões do seu corpo com a razão áurea:
|
Medida A (mA) |
Medida B (mB) |
Razão (mA / mB) |
|
Distância entre o joelho e o umbigo |
Distância entre o joelho e o chão |
|
|
Distância entre o umbigo e o chão |
Distância do topo da cabeça até o umbigo |
|
|
Distância da base do nariz até o queixo |
Distância da linha dos olhos até a base do nariz |
|
|
Distância da metade do pescoço até o umbigo |
Distância do topo da cabeça até a metade do pescoço |
|
O número e (neperiano)
Números
Transcendentes
(em construção)
Aprofunde-se:
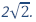
Nenhum comentário:
Postar um comentário