Funções Polinomiais

Na Matemática, bem como em outras ciências, muitas vezes estabelecemos relações entre conjuntos, comumente estamos estabelecendo relações entre grandezas variáveis. A variação é uma importante ideia matemática que pode ser explorada usando as ferramentas da álgebra.

 

No caso em que a relação apresentar a especificidade de que cada elemento do primeiro conjunto se relacionar a um único elemento correspondente no segundo, a relação será denominada de função.

 

As funções polinomiais são usadas com maior frequência na modelagem de fenômenos reais, para isso é preciso aprender a reconhecer uma função polinomial, ou simplesmente polinômio, identificar o grau desta função e calcular o valor numérico da mesma. Assim, estudando essas funções em razão de sua importância dentro da matemática e demais áreas nos tornará aptos a compreender como funcionado diversos mecanismos utilizados nos sistemas financeiros, comerciais, industriais e científicos. Esse estudo aborda as operações aritméticas do conceito de polinômio, assim como as propriedades desse elemento matemático. As funções polinomiais, a priori, formam um plano conceitual importante na álgebra, entretanto possuem também uma relevante importância na geometria, quando se deseja calcular expressões que envolvem valores desconhecidos, como no campo da Geometria Analítica.

 

Por motivos óbvios, damos o nome de função polinomial a uma função que é definida por um polinômio. 

Definição: Seja dado um número inteiro não negativo n, bem como os coeficientes reais a₀, a₁,⋯,a_n, com a_n ≠ 0. A função definida por:

p(x) = a_n ∙ xⁿ + a_n−1  ∙ xⁿ⁻¹ + ⋯ + a₁ ∙ x + a₀

 é denominada função polinomial de grau n, com relação a x.

Onde:

a_n, a_n-1, a_n-2, ..., a₂, a₁, a₀ são chamados coeficientes.

a₀ é chamado termo independente.

n   é denominado o grau do polinômio.

x é a variável e pode assumir quaisquer valores reais ou não reais.

 

EXEMPLO 01:

São exemplos de funções polinomiais:

a) p(x) = 4x + 5  ®   a₀ = 5, a₁ = 4

b) p(x) = x² – 2x + 8  ®  a₀ = 8, a₁ = –2, a₂ = 1

c) p(x) = x³ + 4x² + x – 1  ®  a₀ = –1, a₁ = 1, a₂ = 4, a₃ = 1

d) p(x) = x⁶ – 2  ®  a₀ = –2, a₁ = a₂ = a₃ = a₄ = a₅ = 0, a₆ = –2

 

GRAU DE UM POLINÔMIO:

Dado um polinômio p(x) = a_n ∙ xⁿ + a_n−1  ∙ xⁿ⁻¹ + ⋯ + a₁ ∙ x + a₀, com n , dizemos que o grau de um polinômio é o expoente máximo que ele possui, isto é, se o coeficiente a_n ≠ 0, então o expoente máximo n é dito grau do polinômio e indicamos gr(p) = n.

 

EXEMPLO 02

a) P(x) = 5 ou P(x) = 5x⁰ é um polinômio constante, ou seja, gr(P)= 0.

b) P(x) = 3x + 5 é um polinômio do 1º grau, isto é, gr(P) = 1.

c) P(x) = 4x⁵ + 7x⁴ é um polinômio do 5º grau, ou seja, gr(P) = 5.

Observação: Se P(x) = 0, não se define o grau do polinômio.

 

VALOR NUMÉRICO:

O valor numérico de um polinômio P(x) para x = a, é o número que se obtém substituindo x por a e efetuando todas as operações indicadas pela relação que define o polinômio.

EXEMPLO 03:

Se P(x) = x³ + 2x² + x – 4, o valor numérico de P(x), para x = 2, é:

Resolução:

P(x) = x³ + 2x² + x – 4, substituindo o x por 2, teremos:

P(2) = (2)³ + 2∙(2)² + (2) – 4, resolvendo a expressão, verificamos que:

P(2) = (2)³ + 2∙(2)² + (2) – 4

P(2) = 8 + 2 x 4 + 2 – 4

P(2) = 8 + 8 + 2 – 4

P(2) = 14

 

RAIZ:

Um número complexo r é raiz de um polinômio p(x) quando ao substituir x por r na equação e efetuarmos os cálculos, obtemos p(r) = 0.

EXEMPLO 04:

O número 4 é uma raiz da equação x³ – 6x² + 10x – 8 = 0, pois ao substituir x por 4 temos: 

4³ –  6 ∙(4)² + 10∙(4) – 8 = 64 – 96 + 40 – 8 = 0

 

EXEMPLO 05:

Sabendo-se que –3 é raiz de P(x) = x³ + 4x² – ax + 1, calcular o valor de a.

Resolução:

Se –3 é raiz de P(x), então P(–3) = 0. Ou seja, substituindo x por –3, temos:

P(–3) = 0   (–3)³ + 4∙(–3)² - a∙(–3) + 1 = 0, assim:

–27 + 4∙9 + 3a + 1 = 0, ou seja,

+ 3a +36 –27 + 1 = 0

3a + 10 = 0,

3a =–10

 a = –10/3

 Assim o valor de a é –10/3.

  

Atividades:

1) Considere o polinômio p (x) = 3x² –  x + 5.

a) Calcule p(2):

b) Calcule p (–3):

c) Diga qual é o grau deste polinômio:

 

2) Verifique se 2 é raiz do polinômio p(x) = x² – 5x + 6.

 

3) Sabendo que 6 é a raiz do polinômio p(x) = x² – mx + 6. Calcule o valor de m.

 

Parte 2  - FUNÇÃO

Na maioria das vezes as funções envolvem conjuntos numéricos e alguma lei de formação que as regem.

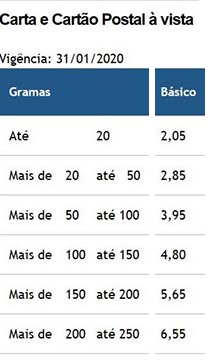
Observe no exemplo apresentado na Tabela a seguir, que relaciona o peso da correspondência com as tarifas praticadas pelo correio brasileiro para o envio de carta comercial e cartão-postal.

Essa tabela nos permite encontrar respostas a várias perguntas, tais como:

ü  Qual o valor a ser pago por uma carta que pesa 73g?

ü  Qual o peso máximo de uma carta para que sua tarifa não ultrapasse R$ 1,00?

ü  É possível que duas cartas com tarifas diferentes tenham o mesmo peso?

ü  É possível que duas cartas com pesos diferentes tenham a mesma tarifa?

Observe que, nesta relação, o peso da carta é a variável independente, e a tarifa, a variável dependente. Podemos notar, ainda, que a cada peso de carta a ser enviada corresponde uma única tarifa. A tarifa depende do peso da carta.

Para facilitar a visualização e compreensão do comportamento de um fenômeno em estudo, as relações ou funções geralmente são expressas em tabelas ou gráficos.

A relação que é denominada por função, portanto, tem

algumas características especiais:

ü  a todos os valores da variável independente estão associados algum valor da variável dependente; e

ü  para um dado valor da variável independente está associado um único valor da variável dependente.

As relações que têm essas características são chamadas funções. Assim, podemos dizer que a tarifa postal é dada em função do peso da carta.

Em outras palavras, podemos dizer que uma função é uma

relação entre dois conjuntos de variáveis de tal modo que, a cada valor do primeiro conjunto, associamos exatamente um valor do segundo conjunto.

Logo, dados dois conjuntos A e B não vazios e f uma relação de A em B. A relação f será uma função de A em B quando a cada elemento x do conjunto A está associado um e apenas um elemento y do conjunto B.

Usualmente denominamos de x a variável independente, e y é a denominação utilizada para a variável dependente.

 

Observe que uma equação pode representar uma função.

Por exemplo, a equação y = 2x + 5 representa uma função.

A notação mais utilizada para expressar uma função é f(x). Assim, teríamos f(x) = 2x + 5.

Mas, como vimos anteriormente, uma tabela também pode expressar uma relação que é uma função.

Diante da correspondência entre um conjunto de valores de x, denominado domínio da função e valores um conjunto de valore de y, denominado imagem da função dizemos que y = f(x), e o par (x, y) é a correspondência dos valores da função.

A notação f(x) é lida como “f de x”. O número representado por f(x) é o valor da função f em x.

       

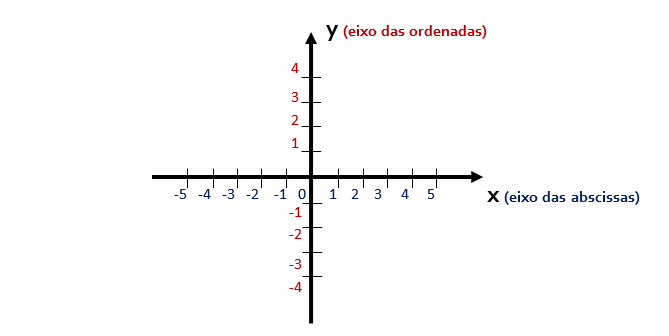
De outro modo, uma função pode ser representada graficamente, para isso é utilizado o plano cartesiano, que é constituído por:

• Um eixo horizontal, no qual os números crescem da esquerda para a direita, é usado para indicar o valor de x. Esse valor também é chamado abscissa, ou simplesmente coordenada x.

• Um eixo vertical, com valores que aumentam de baixo para cima, é usado para representar a coordenada y, também conhecida como ordenada.

  

A localização de cada ponto no plano tem como referência um par ordenado de números reais em que o primeiro elemento se relaciona ao eixo horizontal, denominado de abscissa, e o segundo elemento se relaciona ao eixo vertical, denominado de ordenada do ponto. O par ordenado se denomina coordenada do ponto.

Um par (x, y) é dito par ordenado se seus elementos têm uma ordem fixa.

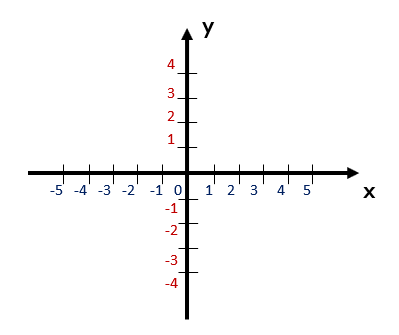
Os eixos coordenados dividem o plano Cartesiano em quatro partes, chamadas quadrantes.

      

1º quadrante: x > 0 e y > 0

2º quadrante: x < 0 e y > 0

3º quadrante: x < 0 e y < 0

4º quadrante: x > 0 e y < 0

 

A abaixo mostra a numeração usada para identificar esses quadrantes. Observe que o primeiro quadrante é aquele no qual os pontos têm coordenadas x e y positivas. Para indicarmos um ponto P do plano, usamos a notação P(x,y). Assim, por exemplo, o ponto A(2,3) tem abscissa 2 e ordenada 3. Esse ponto é mostrado na Figura abaixo, que também contém os pontos B(1,5;−3) e C(−3,1). Ainda na Figura abaixo, percebemos a presença dos pontos D, E, F e G. Com o auxílio das retas horizontais e verticais apresentadas em tom azul claro (que foram traçadas apenas para facilitar a leitura das abscissas e ordenadas), percebemos que as coordenadas desses pontos são D(0,5; 2), E(−2, −4), F(0, −2), e G(1,0).

A função f(x) = 2x + 5 pode ser representada no gráfico, utilizando os pares (x, y) apresentados na tabela e marcando os pontos correspondentes da seguinte forma:

(–2, 1)

(–1, 3)

(0, 5)

(1, 7)

(2, 9)

Uma vez que a coordenada x pode assumir qualquer valor real, o mesmo acontecendo com a coordenada y, podemos definir um número infinito de pares ordenados (x, y).

 

E o que é necessário para esboçar o gráfico de uma função?

Nem sempre temos à mão recursos como programas de computadores e calculadoras científicas para construção de um gráfico; portanto, conhecermos alguns pontos especiais desta representação nos possibilita encontrarmos uma boa aproximação do gráfico da função.

E lembre-se: nesta representação é importante identificarmos os pontos em que o gráfico intercepta os eixos. Sempre considerando que:

ü  Os pontos sobre o eixo das abscissas são do tipo (x,0), isto é, y = 0; e

ü  Os pontos sobre o eixo das ordenadas são do tipo (0,y), isto é, x = 0.

Vale lembrarmos, ainda, que os valores de x em que f(x) = 0 (ou seja, y = 0) são chamados de zeros, ou raízes da função.

 

Assim para representar graficamente uma função:

1° passo: atribuindo valores a x (por exemplo: −3, −2, −1, 0, 1, 2), encontraremos a respectiva imagem. Claro que poderíamos atribuir a x alguns valores fracionários, mas para facilitar a construção do gráfico atribuímos valores mais convenientes, ou seja, atribuiremos alguns valores inteiros.

2° passo: agora vamos representar os pares ordenados, encontrados na tabela de atribuição de valores, por pontos no plano cartesiano.

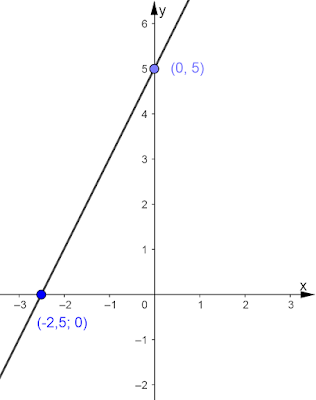
3°passo: trace o esboço do gráfico ligando os pontos encontrados e que satisfazem a lei. Perceba que o gráfico a função y = 2x + 5 é uma reta.

 

Como a lei da função é uma equação que possui duas variáveis, chamamos esse tipo de função de polinomial e dependendo do grau do polinômio recebe nomes especiais:

a) A função f(x) = ax + b (a≠ 0; b≠ 0) recebe o nome de função afim. Tomando como exemplo a função f(x) = 2x + 5, então a = 2 e b = 5. E a sua representação gráfica será uma reta, como já apresentada.

 

b) A função f(x) = ax é denominada função linear. Por exemplo, f(x) = 2x  e a = 2. O gráfico é representado como a reta abaixo:

  

c) A função f(x) = x é denominada função identidade. A função identidade associa um valor do domínio x com o mesmo valor na imagem.

 

d) A função f(x) = k recebe o nome de função constante. Por exemplo, f(x) = 2.

 Observe que a função constante associa a cada valor x um mesmo valor na imagem, que neste exemplo é o 2.

 

e) A função polinomial f(x) = ax² + bx + c com a≠0 recebe o nome de função quadrática, e sua representação gráfica é uma curva denominada parábola.

Veja abaixo a representação gráfica de f(x) = x².

 

É importante destacarmos ainda que:

ü  A representação gráfica das funções polinomiais: afim, linear, identidade e constante é uma reta.

ü  Podemos pensar que a função linear f(x) = ax e a função identidade f(x) = x são casos particulares da função afim f(x) = ax + b.

A seguir, apresentamos outro exemplo de tabela que também representa uma função:

É possível representar essa função por uma lei que rege a relação (por uma regra):

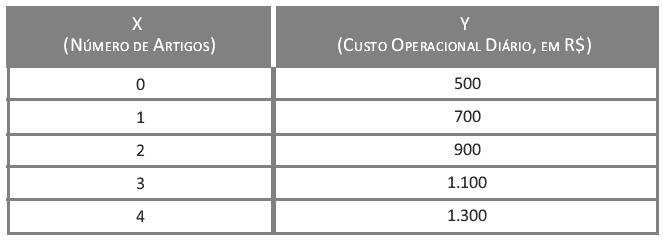
Para obter o custo operacional diário no exemplo exposto

anteriormente na forma de tabela, para 0, 1, 2, 3 ou 4 unidades, multiplique o número de itens por 200 e adicione 500 ao resultado.

Dessa ideia expressa, é possível também expressar algebricamente por uma equação:

Para obter o custo diário no exemplo anterior, temos y = 200x + 500, em que x é o número de artigos e y é o custo operacional diário.

E obteremos o seguinte gráfico:

 Observações importantes:

a) Nem toda relação pode ser considerada uma função.

Acompanhe o exemplo: seja R o conjunto dos funcionários de um órgão público que constam da lista telefônica da cidade M. Seja T o conjunto de números de telefone dos residentes na cidade M que constam da lista telefônica.

Será que a relação que associa os elementos de R ao correspondente elemento em T é uma função?

Alguns funcionários têm mais de um número de telefone.

Assim, a relação não é uma função.

Fique atento! Embora uma função possa ser representada por uma equação, nem toda equação representa uma função.

b) Observe que nem toda representação gráfica representa uma função!

Para rapidamente identificarmos se um gráfico é uma função, basta imaginarmos retas verticais, paralelas ao eixo das ordenadas “y”, passando pelos elementos do domínio.

Se todas as retas que imaginarmos tocarem o gráfico em apenas um ponto, será uma função. Isto porque com este recurso identificamos que, para cada x (elemento do domínio), associa-se apenas um y (imagem de x).

Atividades:

1) Um fabricante de automóveis realizou um teste de frenagem de seu novo modelo, obtendo a tabela abaixo, que relaciona a velocidade no instante de início da frenagem à distância que o carro percorre até parar completamente. Represente os dados da tabela como pontos do plano Cartesiano, usando o eixo-x para indicar a velocidade (em km/h) e o eixo-y para fornecer a distância percorrida (em metros).

 

 

2) O prefeito da cidade de Jurerê tomou a saudável decisão de expandir a rede de distribuição do município, para que toda a população fosse servida por água potável.

 Naturalmente, se o projeto da prefeitura levar em conta apenas a população atual do município, é provável que, ao longo das obras, o número de habitantes cresça, e que parte das pessoas permaneça sem acesso à rede de água quando a expansão da rede estiver pronta. Ciente disso, a companhia municipal de saneamento decidiu usar um modelo matemático baseado no censo demográfico do IBGE para prever o crescimento da população, de modo a garantir que, em 2020, todos os munícipes tenham água encanada. 

Para estimar a população futura de Jurerê, a companhia de saneamento fez uma estratégia usada pela companhia análise matemática dos dados do IBGE, e obteve a seguinte equação, que associa de saneamento para encontrar a equação que relaciona P a t, sendo P o número de habitantes e t o tempo, em anos, transcorrido desde 2000: 

P = 12.000 + 360t.

a) Qual será a população quando t = 8 anos.

b) Usando essa estratégia, calculou-se a população em vários anos, e reuniu essas informações na Tabela:

Represente o gráfico da função a partir dos dados da tabela:

 

3) Uma indústria adquiriu uma máquina por 175 mil reais. Em decorrência da obsolescência e do desgaste por uso, a cada ano, a máquina perde 25 mil reais de valor. Desse modo, podemos dizer que o valor da máquina, v (em R$ 1.000), é dado pela equação v = 175 − 25t, em que t é o número de anos decorridos desde sua aquisição.

a) Monte uma tabela com o valor da máquina para t = 0, 1, 2, 3 e 4.

b) Trace um gráfico que relacione o valor da máquina (em milhares de reais) à sua idade (em anos).

c) A máquina atinge sua vida útil, e precisa ser substituída, quando seu valor se reduz a R$ 20.000. Determine a vida útil dessa máquina.

 

4) Para alugar um determinado carro por dois dias, a locadora Saturno cobre R$ 80,00 de taxa fixa e R$ 0,75 por quilômetro rodado. Nesse caso, o custo C do aluguel (em R$) é dado pela expressão 

C = 80 + 0,75x, 

em que x é a distância percorrida pelo carro (em km).

a) Qual a distância percorrida por um usuário se ele pagou R$ 185,00.

b) Determine o custo para x = 0 e x = 200 e trace o gráfico correspondente à função a partir desses valores.

 

5) Se um carro partir do quilômetro 25 de uma estrada, e viajar a uma velocidade constante de 60 km/h, a sua posição na estrada (ou seja, o quilômetro no qual o carro se encontra) no instante t (em horas) será dada pela expressão 60t + 25. Determine, graficamente, o tempo que o carro gastará para chegar ao quilômetro 175 da referida estrada.

 

6) Trabalhando em uma loja de roupas, Gláucia recebe R$ 1.200,00 de salário mensal fixo, além de uma comissão de R$ 0,09 para cada real vendido.

a) Determine uma equação que expresse o valor recebido por Gláucia em relação ao valor dos produtos que ela vende em um mês.

b) Se, no mês passado, Gláucia recebeu R$ 2.280,00 de salário, calcule quantos reais em roupas ela conseguiu vender.

 

7) O administrador de um Museu lançou uma campanha publicitária para aumentar o número de visitantes.

Após o início dessa campanha, ele percebeu que o número de visitantes foi aumentando mensalmente segundo uma progressão aritmética. Veja a seguir as anotações, relativas aos três primeiros meses de campanha, feitas por esse administrador.

  

Suponha que esse aumento continuará durante um ano de campanha. Sendo n o número do mês da campanha e v o número de visitantes, qual é a expressão que permite calcular o número de visitantes em cada mês?

        (A) v = 600n + 5.000   

        (B) v = 600n + 5.600 

        (C) v = 1.200n + 4.400   

        (D) v = 5.000n + 600 

8) Numa corrida de táxi , é cobrada a taxa fixa de R$ 2,00 mais R$ 1,50 por quilômetro rodado.

a) Se a corrida for de 15 km, qual será o valor a pagar? E se a corrida for de 10 km?

b) Qual é a sentença que dá o valor a pagar (y) em função da quilometragem percorrida (x) ?

c) Se um passageiro pagou R$ 12,50, qual foi a distância percorrida pelo táxi?

d) Esboce o gráfico da equação obtida.

9) Vamos supor que o preço a ser pago por uma viagem de táxi inclua uma bandeirada de R$ 3,44 e um custo de R$ 0,90 para cada quilômetro rodado.

a) Escreva uma função C que forneça o custo, em reais, de uma corrida de x quilômetros.

b) Determine o custo de uma viagem de 8,5 km, bem como custo o de uma viagem de 12 km.

Aprofunde-se: