O objetivo da Geometria Analítica é dar um tratamento algébrico às representações geométricas, para isso usa-se como ferramenta, o que chamamos de Plano Cartesiano, que é o conjunto de duas retas, uma horizontal e outra vertical, orientadas a partir de uma origem.
Vejamos,
a princípio, o que é uma reta orientada, e suas características.
Uma
reta é chamada de orientada quando cada ponto corresponde a um número real e
vice-versa, tendo como origem de sua orientação um ponto que iremos definir
como o correspondente ao 0 (zero).
Para
representação de uma reta orientada ou eixo, vamos escolher:
a)
Um ponto O na reta como origem, associado ao 0;
b)
O lado direito à origem é o sentido positivo, onde crescem os números, e o lado
esquerdo à origem é o sentido negativo.
Na
figura dada, o ponto A corresponde ao número 1 e o ponto B corresponde ao .
O número associado a cada ponto é
denominado abscissa desse ponto.
A abscissa do ponto O é 0.
A abscissa do ponto C é –3 .
A abscissa do ponto D é –1/2.
O que é distância entre dois pontos?
Tomamos como unidade de medida, entre os pontos de uma reta, a distância de um número inteiro ao seu consecutivo. Dizemos, por exemplo, que a distância entre 0 e 1 é 1, entre –3 e –2 é 1.
Observe, na reta acima, a distância entre os pontos O e C é 3
unidades, e a distância entre os pontos A e C é 4 unidades.
De modo geral, a distância entre
dois pontos quaisquer na reta A e B, de abscissas a e b, respectivamente, é
dada por: d(A, B) = |b – a|, o módulo da diferença entre as
abscissas de A e B.
Exemplo: Sabendo que na reta real os pontos A, B e C têm abscissas –4, –1 e 3, respectivamente, podemos calcular as distâncias d(A, B), d(B,C) e d(A,C) entre os pontos.
Fazendo o módulo da diferença entre as abscissas dos pontos, temos:
d(A,B) = |–4 –(–1)| = |–3| =
3
d(B,C) = |–1 – 3| = |–4| = 4
d(A,C) = |–4 – 3| = |–7| = 7
Notemos que a distância será
sempre um número real não-negativo e
que representa o comprimento do segmento,
que neste caso, serão AB, BC e AC.
Outro exemplo: Sabendo que o comprimento de um segmento MN é 4, e que na reta a abscissa de M é 3, podemos calcular a abscissa de N.
Fazendo o módulo da diferença entre as
abscissas, e considerando a abscissa de N uma incógnita n, temos:
MN = |3 – n| = 4.
Resolvendo a equação modular:
3 – n
= 4
n = 3 – 4
n
= –1
ou
3 – n
= –4
n = 3 + 4
n
= 7
Então,
neste caso, há duas possibilidades para a abscissa de N, –1 e 7.
Notemos que N1 e N2 têm a mesma distância ao ponto M, ou seja, simétricos em relação a M.
Ponto no Plano Cartesiano
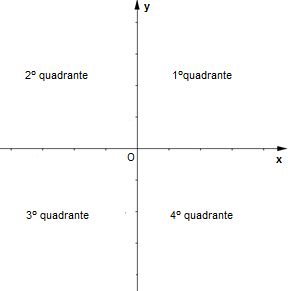
O Plano Cartesiano é constituído por duas retas orientadas, uma horizontal e outra vertical, que são chamadas de eixos, Ox e Oy, respectivamente; perpendiculares entre si e com mesma origem O.
O eixo x ou Ox é o eixo das abscissas.
Note que os eixos dividem o plano em quatro regiões denominadas quadrantes, cuja identificação é feita no sentido anti-horário.
Sistemas de Coordenadas Cartesianas
Quando num plano cartesiano, podemos localizar pontos,
tanto nos quadrantes como nos eixos, e fazer correspondências entre o plano e
esses pontos, temos ai um sistema de coordenadas cartesiana.
Para determinarmos as coordenadas de um ponto P no plano, traçamos linhas perpendiculares aos eixos x e y.
Neste
caso, a é a abscissa do ponto P; b é a ordenada do ponto P; a e b
constituem as coordenadas do ponto P.
As
coordenadas do ponto P são representadas através do par ordenado P(a, b).
Par Ordenado
Todo
par ordenado (a, b) de números reais fica
associado a um único ponto P no plano, e todo ponto P do plano fica determinado
quando são dadas a abscissa a e a
ordenada b.
O ponto A tem abscissa 2 e ordenada 3, então ele está associado ao par ordenado (2, 3).
Do mesmo
modo, o ponto B está associado ao par ordenado (–1, 2) e o ponto C está associado ao par
ordenado (1, –1).
Quadrantes
Em
relação aos quadrantes, podemos notar que, o ponto P que se encontra no:
a) 1o quadrante, tem abscissa e ordenada positivas;
b) 2o
quadrante, tem abscissa negativa e ordenada positiva;
c) 3o
quadrante, tem abscissa e ordenada negativas;
d) 4o
quadrante, tem abscissa positiva e ordenada negativa.
Como o ponto A(2, 3) tem abscissa e ordenada positivas, então ele está no 1o quadrante. Bem como, um ponto D(–2,–3) está localizado no 3o quadrante, pois tem abscissa e ordenada negativas.
Pontos nos eixos
Se um ponto P estiver localizado no eixo x, a sua ordenada é 0. Assim como, se um ponto P estiver localizado no eixo y, sua abscissa é 0.
Na figura, o ponto A tem abscissa 2 e está sobre o eixo x, então ele está associado ao par ordenado (2, 0).
O ponto
B tem ordenada 3 e está sobre o eixo y,
então ele está associado ao par ordenado (0, 3).
E o
ponto C está associado ao par ordenado (0, –1).
Distância entre dois pontos no Plano
Observe a figura:
As coordenadas do ponto A são abscissa 2 e ordenada
3, ou seja, A(2, 3).
Temos também D(2, 0) e E(0, 3).
Para determinar a distância entre os pontos A(2, 3) e D(2, 0), basta fazer o módulo da diferença das suas ordenadas, já que têm a mesma abscissa; assim d(A, D) = |3 – 0| = 3.
Também ocorre com a distância entre os pontos A(2, 3) e E(0, 3), fazemos a diferença entre os módulos das suas abscissas, já que têm a mesma ordenada, assim d(A, E) = |2 – 0| = 2.
De modo geral, se dois
pontos P(a, b) e Q(a, c) têm a mesma abscissa e ordenadas
diferentes, então a distância entre os pontos será o módulo da diferenças
das suas ordenadas, e temos: d(P, Q)
= |b – c|.
Agora, se dois pontos P(a, b) e Q(c, b) têm a mesma ordenada e abscissas diferentes, então a distância entre os pontos será o módulo da diferenças das suas abscissas, e temos: d(P, Q) = |a – c|.
Exemplos: Calculando a distância entre
os pontos A(3, 4) e B(9, 4).
Observe que, os pontos têm a mesma ordenada 4, então a distância entre eles será o módulo da diferença de suas abscissas e teremos:
d(A, B) = |9 – 3| = 6.
Agora, calculando a distância entre os pontos C(–2, –3) e D(–2, 4).
Observe que, os pontos têm a mesma abscissa –2,
então a distância entre eles será o módulo da diferença de suas ordenadas e
teremos:
d(C, D) = |– 3 – 4| = |–7| = 7.
Notando a mesma figura:
Se quisermos calcular a distância entre D(2, 0) e
E(0, 3) que têm, entre si, abscissas e ordenadas diferentes, igualmente
como se quisermos d(A, B), d(A, C) ou d(B, C); deveremos utilizar o Teorema de
Pitágoras, que diz: “Num triângulo retângulo, a soma do quadrado da hipotenusa
é igual a soma dos quadrados dos catetos.”
Na figura, vemos que a distância d(D, E) é o
comprimento do segmento DE, que é a hipotenusa do triângulo retângulo ADE.
Utilizando o teorema de Pitágoras no triângulo
retângulo formado no plano:
Temos que, os segmentos AD = 3 e AE = 2 são os
catetos do triângulo retângulo ADE, e queremos saber o comprimento hipotenusa
DE = x.
Aplicando o teorema de Pitágoras, temos: x2 = 32 + 22.
Resolvendo a equação: x2 = 9 + 4 = 13
x =
3,6.
De modo geral, a distância entre dois pontos P(x1, y1) e Q(x2,
y2), formando um triângulo
retângulo no plano e obtendo o comprimento dos catetos através da
diferença das abscissas (x2
– x1) e a diferenças das
ordenadas (y2 – y1), é dado por:
Exemplo: Calcule a distância entre B(–1, 2) e C(1, –1):
a) obtendo
o comprimento dos catetos, com a diferença das abscissas (–1 – 1) e a diferença
das ordenadas (–1 – 2)
b) d(B,C) =
Atividades:
1) Dada a reta real da figura,
calcule:
a) d(A, B) =
b) d(A, C) =
c) d(B, C) =
d) d(C, A) =
2) Sabendo que a distância
entre os pontos A e B é 6, calcule a abscissa m do ponto B da figura abaixo:
3) Sabendo que a distância
entre os pontos M(3) e N(a) é igual a
7, calcule o valor de a.
4) A distância entre dois
pontos A e B, localizados sobre o eixo das abscissas, é 10. Sabendo que a
abscissa A é –7, calcule a abscissa de B.
5) Localize, no plano
cartesiano, os pontos: A(0, 3), B(–2, 1), C(0, –2) e D(3, 1).
a) Verifique se os pontos
estão alinhados.
b) Trançando as retas AB e CD,
verifica-se que elas são paralelas ou concorrentes?
c) Calcule d(A, C) e d(B, D).
6) Calcule o valor de k para que o ponto P(–5, 2k – 8) pertença ao eixo horizontal do
sistema cartesiano ortogonal.
7) Determine x para que o ponto M(2x + 4, 5) pertença:
a) ao 2º quadrante;
b) ao 3º quadrante;
8) Sejam os pontos: A(5, –3),
B(0, 9), C(5, 7) e D(–2, 7). Calcule:
a) d(A, B) =
b) d(B, C) =
c) d(B, D) =
d) d(C, D) =
9) Na figura abaixo, calcule o
perímetro do triângulo:
10) Calcule o perímetro de um
triângulo de vértices A(–1, 0); B(2, –3) e C(2, 3).
11) Calcule o perímetro do
quadrilátero ABCD de vértices:
A(–1, 0); B(0, –2); C(3, 0) e
D(0, 4).
12) A distância do ponto P(a,
1) ao ponto A(0, 3) é igual a 5. Calcule o número a.
13) Determine o ponto E, pertencente
ao eixo Oy, que dista igualmente dos pontos A(2, 3) e B(6, 5)
14) Sabe-se que P(a, 2) é equidistante dos pontos A(3, 1) e B(2, 4). Calcule a
abscissa a do ponto P.
15) Em um exercício militar ,
um submarino parado em um ponto O do mar totalmente submerso tem a missão de
navegar até o ponto B.
Para no ser localizado, o
comandante desligou os equipamento de emissão e recepção de sinais e se preparou
para a navegação manual.
Para isso estabeleceu um
sistema cartesiano de origem O adotando quilometro como a unidade nos eixos,
eixo Oy no sentido norte, e o eixo Ox no sentido leste.
Em seguida navegou verticalmente 2,4 km em linha reta no sentido norte e,
depois 1 km em linha reta no sentido oeste estacionando exatamente no
ponto B.
a) Determine as coordenadas do
ponto B em relação ao sistema cartesiano adotado pelo comandante?
b) Que distância percorreu o submarino no trajeto descrito?
c) Que distância teria percorrido o submarino se fosse em linha reta de
O até B?
16) Ao mapa de uma região
plana foi associado um sistema cartesiano de coordenadas, cuja unidade adotada
em cada eixo é o quilômetro. O ponto E(–6, 4) representa uma empresa de
entregas, que localiza com seus motoboys via GPS, cujo alcance é de
23km.
a) A empresa conseguirá localizar
o motoboy, quando ele estiver no
ponto P(6,
–12)? Por que?
b) A empresa conseguirá se
comunicar com o motoboy quando ele
estiver no ponto M(14,16)? Por que?
17) Devido ao aumento do fluxo de passageiros, uma empresa de transporte coletivo urbano está fazendo estudos para a implantação de um novo ponto de parada em uma determinada rota. A figura mostra o percurso, indicado pelas setas, realizado por um ônibus nessa rota e a localização de dois de seus atuais pontos de parada, representados por P e Q.
Os estudos indicam que o novo
ponto T deverá ser instalado, nesse
percurso, entre as paradas já existentes P e Q, de modo que as distâncias
percorridas pelo ônibus entre os pontos P e T e entre os pontos T e Q sejam iguais.
De acordo com os dados, as
coordenadas do novo ponto de parada são:
(A) (290, 20)
(B) (410, 0)
(C) (410, 20)
(D) (440, 0)
(E)
(440, 20)
















Nenhum comentário:
Postar um comentário