A potenciação indica multiplicações de fatores iguais. Por exemplo, o produto 4 x 4 x 4 pode ser indicado na forma 43.
Com 4 na base da potência e 3 como expoente da potência.
Veja mais exemplos:
23 = 2 x 2 x 2 = 8.
(–3)2 = (–3) x (–3) = 9.
(–5)3 = (–5) x (–5) x (–5) = –125.
De modo geral:
Também
podemos definir que em uma potência:
a)
com expoente 1 e base igual a um número real qualquer, o resultado é esse
próprio número;
b)
com expoente 0 e base igual a um número real diferente de zero, o resultado é
1.
c) com expoente igual a um número inteiro negativo e base diferentes de zero, o resultado é o inverso elevado ao oposto desse expoente, ou seja:
Observe alguns exemplos:
a) 4–2 + 2–4 =
b) 5–2 x 102 =
c) 6–2 x 23 x 32 =
d) (–2)2 – 2 =
P1. Produto de potências de mesma base
Considere o exemplo 42 x 46. Por definição de potência temos:
42 x 46 = (4 x 4) x (4 x 4 x 4 x 4 x 4 x 4) = 48.
De modo geral, sejam a ≠ 0 e m e n números reais, então am ∙ an = am + n.
Exemplos:
42 x 46
= 42 + 6 = 48.
(–5)3 x (–5)4
= (–5)3 + 4 = (–5)7.
a6 ∙ a
–2 = a6 + (–2) = a6 – 2 = a4.
32 x 34
x 33 = 32 + 4 + 3 = 39.
P2. Divisão de potência de mesma base
Considere o exemplo

Treine, agora, com as seguintes potências:
P3. Potência de potência
Considere o seguinte exemplo (53)2. Pela definição de potência temos:
(53)2 = 53 x 53 = (5 x 5 x 5) x (5 x 5 x 5) = 56 = 15.625.
De modo, geral, sejam a ≠ 0 e m e n números reais, então (am)n = am ∙ n.
Exemplos:
|
31 = 3 |
|
36 = 729 |
|
32 = 9 |
|
37 = 2.187 |
|
33 = 27 |
|
38 = 6.561 |
|
34 = 81 |
|
39 = 19.683 |
|
35 = 243 |
|
310 = 59.049 |
27 x 2.187 =
19.583 : 729 =
812 =
Se a tabela agilizou os
cálculos, imagine o que não faria uma calculadora eletrônica.
Há quatrocentos anos, os matemáticos
não sonhavam com calculadoras. Nem mesmo essas tabelas eles conheciam.
Mas, no século XVI, com o
desenvolvimento da Astronomia, da navegação e do comércio, os cálculos
tornaram-se longos e trabalhosos.
Essas dificuldades levaram os
matemáticos da época a buscarem alternativas. E tiveram uma grande ideia.
2) Uma espécie de bactéria dobra
a população a cada dia e uma cultura tem 100 indivíduos inicialmente. Sabendo
que 25 = 32 e 26 = 64, vamos estimar quantos dias levará
para que a população:
a) Chegue a 3.200?
b) Chegue a 6.400?
c) Chegue a 204.800?
d) Chegue a 6.553.600?
3) Escreva em forma de potência o
valor:
a) do dobro de 29.
b) da metade de 29.
c) do quadrado de 29.
d) do triplo de 37.
e) da terça parte de 37.
f) do quadrado de 37.
g) do cubo de 37.
h) do quádruplo de 24.
5) Calcule o valor da
expressão 5x ∙
5x – 1 ∙ 5x + 1.















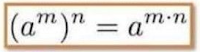




Nenhum comentário:
Postar um comentário