Ligados principalmente à contagem de situações ocorridas na natureza esses números foram chamados de naturais e podem ser reunidos em um conjunto indicado pela letra N.
Nem sempre a contagem dos elementos de um conjunto é feito de forma direta, contando cada elemento do conjunto. Vejamos:
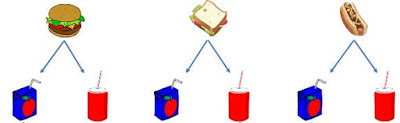
1) Uma lanchonete oferece três tipos de sanduíches (carne, frango e salsicha) e dois tipos de bebidas (suco de laranja e refrigerante de guaraná). Quantos lanches diferentes podem ser oferecidos, se cada um deve conter um sanduíche e uma bebida?
2) Se Monica tivesse cinco vestidos, quatro tênis e três meias, todos os itens diferentes um do outro. De quantas maneiras diferentes ela poderia se vestir?
3) Num smartphone protegido por senha de quatro algarismos, de 0 a 9, quantas são as possibilidades de senhas diferentes?
Vamos
considerar que os quadrinhos a seguir são a posição que cada dígito da senha
irá ocupar:
Desse
modo, podemos contar o número de possibilidades de algarismos que pode ser
colocado em cada posição:
a)
para o 1º dígito, temos 10 possibilidades {0, 1, 2, 3, 4, 5,6, 7, 8, 9};
b)
igualmente para o 2º, 3º e 4º dígitos, o mesmo número de possibilidades.
Para cada um dos 10 dígitos possíveis a ser colocados na 1ª posição, temos 10 possibilidades na 2ª posição, tendo assim 10 x 10 = 100 possibilidade até a 2ª posição; e seguindo essa ideia para cada uma das outras é possível também 10 para cada uma das posições anteriores:
Daí, o número total de possibilidades de senha será:
10 x 10 x 10 x 10 = 104 = 10.000.
Portanto, temos 10.000 possibilidades de senhas diferentes.
À essa forma de contagem indireta, damos o nome de Princípio Multiplicativo.
4) O diretor de uma escola convidou alunos de terceiro ano a participarem de uma brincadeira. Suponha que existem 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa. O objetivo da brincadeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido. Quantas são as possibilidades de respostas dados pelos alunos nessa brincadeira?
b) Imagine agora, se fosse possível um cadeado em que o
disco de possibilidades comporta as 26 letras do alfabeto, nesse caso, qual
total de senhas possíveis?
6) Numa lanchonete, é possível montar o próprio sanduíche combinando 5 tipos de pão, 6 tipos de recheio e 3 tipos de molho. Quantos sanduíches diferentes podem ser montados?
7) Em uma lanchonete há 3 tipos de sanduíche, 2 tipos de suco e 2 tipos de sobremesa. De quantas maneiras diferentes pode-se fazer um lanche nessa lanchonete escolhendo 1 sanduíche 1 suco e 1 doce?
8) Fichas podem ser pretas,
brancas ou vermelhas; circulares, quadradas ou circulares; finas ou grossas.
Quantos tipo de fichas existem?
9) Uma montadora de automóveis apresenta um carro em quatro modelos diferentes e em cinco cores diferentes. Um consumidor que quiser adquirir esse veículo terá quantas opções de escolha?
10) Um automóvel é oferecido pelo
fabricante em 6 cores diferentes com 3 tipos de acabamento (standard, sport ou
luxo) e com 3 tipos de motores (1.6, 1.8 e 2.0), sendo que os motores podem ser
movidos a álcool ou a gasolina. Quantas são as opções de escolha de um
comprador desse automóvel?
13) Dez atletas disputam uma
corrida com iguais chances de vencer. De quantos modos diferentes pode ocorrer
a chegada dos 3 primeiros colocados?
14) Um time brasileiro de futebol disputará obrigatoriamente 6 jogos numa excursão pela Europa. De quantos modos diferentes poderá ocorrer a campanha desse time durante essa excursão?
a) Quantas são as possibilidades
de senhas diferentes?
b) Entretanto, um especialista
em sistemas de segurança eletrônica recomendou à direção do banco recadastrar
seus usuários, solicitando, para cada um deles, a criação de um nova senha com
seis dígitos, permitindo agora o uso das 26 letras
do alfabeto, além dos algarismos de 0 a 9. Nesse novo sistema, cada letra maiúscula era considerada
distinta de sua versão minúscula. Além disso, era proibido o uso de outros
tipos de caracteres. Quantas são as possibilidades de senhas nessa nova
configuração?
c) Uma forma de avaliar uma
alteração no sistema de senhas é a verificação do coeficiente de melhora, que é
a razão do novo número de possibilidades de senhas em relação ao antigo. Qual é coeficiente de melhora da alteração recomendada?
Para ir da cidade A à cidade
B, há 4 estradas; da cidade B à cidade C, há 3 estradas; e da cidade C à cidade
D, 2 estradas.
Determine o total de caminhos
possíveis para se ir:
a) de A até C;
b) de D até B.
Todos os alunos decidiram
participar. A cada vez um aluno é sorteado e dá a sua resposta. As respostas
devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser
sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é
declarado vencedor e a brincadeira é encerrada.
O diretor sabe que algum aluno
acertará a resposta porque há:
(A) 10
alunos a mais do que possíveis respostas distintas.
(B) 20
alunos a mais do que possíveis respostas distintas.
(C) 119 alunos
a mais do que possíveis respostas distintas.
(D) 260
alunos a mais do que possíveis respostas distintas.
(E) 270
alunos a mais do que possíveis respostas distintas.
















Nenhum comentário:
Postar um comentário