Revisando Unidades de Medidas de Comprimento e Área

Das ferramentas inventadas pelo homem, a unidade de medição foi uma das primeiras. ... 

Assim, da necessidade do ser humano de gerar uma medição precisa, principalmente para o comércio, um dos primeiros instrumentos de medição de que se tem notícia é a balança, inventada pelos egípcios, 5 mil anos antes de Cristo.

Das ferramentas inventadas pelo homem, a unidade de medição foi uma das primeiras. As sociedades primitivas já realizavam medições rudimentares para diversas tarefas, como: construções de habitações de tamanho e forma apropriados, moldagem de roupas, troca de alimentos ou matérias-primas, entre outros.

Inicialmente, as medidas eram inspiradas no corpo humano. Por exemplo, a unidade mais usada na antiguidade, principalmente pelos egípcios, era o Côvado, distância entre o cotovelo e a ponta do dedo médio. O padrão real desta medida correspondia a 7 palmos ou 28 dedos, equivalente hoje a 52,3 centímetros.

Assim, da necessidade do ser humano de gerar uma medição precisa, principalmente para o comércio, um dos primeiros instrumentos de medição de que se tem notícia é a balança, inventada pelos egípcios, 5 mil anos antes de Cristo. Esta invenção foi de suma importância, pois a economia nesta época era baseada na agricultura e os impostos cobrados, baseados no peso.

Com a evolução dos seres humanos, novas medidas foram se tornando necessárias e novos instrumentos de medida foram sendo criados.

Medir é comparar grandezas de mesma natureza. A medida é uma forma de comparar duas grandezas de mesma espécie, por exemplo, dois comprimentos, duas áreas, dois volumes, duas massas, duas temperaturas, a partir de um modelo chamado padrão de medida.

Atualmente as unidades de medidas utilizadas e padronizadas pelo Sistema Internacional de Unidades de Medidas, que define as diversas espécies de grandezas e suas unidades correspondentes. 

Vamos, neste momento, conhecer algumas unidades padrões, especialmente utilizado nos estudos de Geometria e diversas Ciências.

Uma recomendação médica

Após uma consulta médica, Terezinha é orientada a manter alguma atividade física regular.

A médica foi específica: - “Caminhe três quilômetros por dia, com tênis adequado, roupas leves e se hidratando”!

Terezinha se prepara e vai até a praça. Chegando lá depara-se com um problema. Como saber quantas voltas são necessárias na pista da praça para cumprir a recomendação médica?

Como Terezinha, sem nenhum instrumento de medida, poderá seguir a indicação médica?…

Para responder a essas perguntas, vamos precisar de um planejamento.

a) Reflita um pouco na situação e indique, quais as medidas que Terezinha precisa conhecer para iniciar as recomendações médicas?

b) Tente sugerir três objetos cuja medida seja fácil de obter e que dariam conta do problema. Converse sobre a escolha desses objetos com os outros estudantes.

c) Como a pessoa deve utilizar cada um desses objetos de medida conhecida para resolver o problema?

d) Como a situação envolve conhecer distância percorrida a pé, qual dessas medidas parecem mais adequadas para a resolução do problema:

        (    ) o pé da pessoa.

        (    ) a altura da pessoa.

        (    ) o passo da pessoa.

e) Descreva como, com a escolha feita no item anterior, a pessoa deve proceder para obter a medida que precisa. Compare sua descrição com a de outros estudantes.

f) O que você considera mais adequado: Utilizar a medida escolhida (tamanho do pé, altura ou tamanho do passo) do início ao fim da caminhada, ou seja, até completar os três quilômetros; ou é melhor usar essa medida para obter o comprimento de uma volta na pista e, com isso, contar os três quilômetros?

g) Converse com outros estudantes e cite o que poderia ser medido na sua escola, utilizando a mesma técnica dos três quilômetros de caminhada; escolham, juntos, uma das que foram citadas e realizem essa medição.

h) Por mais quatro vezes, meça o que mediu no item anterior, utilizando a mesma técnica. Essas medidas são todas iguais? Foram iguais para os outros estudantes? Por quê?

i) É provável que você ou os outros estudantes tenham obtido medidas diferentes dentre as cinco medições feitas. Como tratar esses valores com a finalidade de informar para alguém a melhor estimativa para o comprimento investigado?

j) Para melhor adequar essa atividade ao seu tempo disponível, como a pessoa deveria proceder para obter a estimativa de tempo que levará para percorrer os três quilômetros?

I) Comprimento

Uma das primeiras grandezas a ser estuda pelo homem, hoje pode ser medido de várias formas: a régua, a fita métrica, o metro e aparelhos de alta precisão.

Podemos definir a distância entre dois pontos distintos A e B como sendo o comprimento do segmento de reta de extremidades A e B.

A unidade padrão de medida do comprimento é o metro (m). Os múltiplos e submúltiplos do metro mais utilizados são: o quilômetro (km), o decímetro (dm), o centímetro (cm) e o milímetro (mm).

Atividades:

1) Senhor Pitágoras, comprou um terreno com as dimensões indicadas na figura abaixo. Se ele deseja construir um muro em torno do terreno, qual deverá ser a extensão desse muro? 

2) Em média, o passo de Mario mede 50 cm. Qual a distância, em metros, Mario percorre ao dar mil passos?

3) Uma montanha de 0,937 km de altura. Deseja-se construir um edifício com a décima parte da altura da montanha. Quantos metros deve ter o edifício?

4) A avenida Presidente Vargas conecta a região da Leopoldina ao fim da Zona Norte do Rio de Janeiro à região da Candelária numa extensão de 3.501 metros.

Assim, podemos informar que essa avenida possui comprimento de:

             (A) três quilômetros e cinquenta e um metros.

      (B) três metros e meio.

      (C) três quilômetros e quinhentos e um metros.

      (D) três mil metros e quinhentos centímetros

5) Agora, se Senhor Pitágoras desejar construir uma casa de 200 metros quadrados no terreno que comprou, e o restante da área do terreno plantar grama, com essas dimensões ele irá conseguir construir essa casa e plantar grama?

6) Um automóvel percorreu num dia 1,2 km pela manhã, 800 m a tarde e a noite 2,5 km. Podemos dizer que o automóvel percorreu no dia:

        (A) 4,25 km

        (B) 4,5 km

        (C) 8,65 km

        (D) 8,3 km

7) Renato precisa medir a espessura do vidro da janela de sua casa. A unidade mais adequada para realizar essa medida é:

        (A) milímetro. 

        (B) decímetro. 

        (C) metro. 

        (D) quilômetro.

8) Celina comprou 3 metros de tecido para fazer um vestido e 0,5 metros para fazer uma saia. Quantos centímetros de tecido Celina comprou, ao todo, para fazer essas duas peças de roupa?

        (A) 3,5.    

        (B) 35.   

        (C) 350.   

        (D) 3.500.

9) Marcelo costuma correr 12 km ao redor do quarteirão retangular RSTU de 250 m de comprimento por 150 m de largura, representado na figura abaixo. Ele inicia a corrida sempre do ponto P, situado a 150 m do vértice R, correndo no sentido horário, como mostra a figura.

Em qual dos lados do quarteirão Marcelo completa a corrida de 12 km?

        (A) RS.     

        (B) ST.     

        (C) TU.     

        (D) UR.

10) O Sistema Métrico Decimal é o mais utilizado atualmente para medir comprimentos e distâncias. Em algumas atividades, porém, é possível observar a utilização de diferentes unidades de medida. Um exemplo disso pode ser observado no quadro.

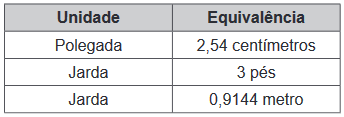
Assim, um pé, em polegada, equivale a:

        (A)   0,1200      

        (B) 0,3048         

        (C) 1,0800        

        (D) 12,0000      

        (E) 36,0000

11) Durante a montagem de uma rede hidráulica, um encanador vai utilizar canos ¾ de polegada. Esses canos devem ser encaixados em sulcos na parede. Os sulcos são feitos por um aparelho que possui uma lâmina metálica e que, ao ser passado sobre a superfície da parede, produz o sulco. Sabendo que uma polegada equivale a 2,54 cm, a lâmina metálica deve apresentar uma largura mínima igual a:

        (A) 1,90 mm.     

        (B) 7,62 mm.      

        (C) 10,55 mm.   

        (D) 19,05 mm.

A lotação no restaurante

Um empresário encontrou um lugar que parecia estar adequado aos seus planos de montar um restaurante. Com a finalidade de tomar sua decisão sobre a aquisição ou não deste lugar, precisava de mais detalhes que só uma visita poderia fornecer. Pediu ao seu irmão mais novo que visitasse o lugar e lhe trouxesse informações de que precisava. Enviando seu irmão mais novo, ao invés de uma pessoa especializada, o empresário tem a intenção de ajudar seu irmão a adquirir experiência em empreendedorismo.

O irmão mais novo retornou da visita com a figura a seguir e afirmou: - “Esta é a vista de cima da região destinada às mesas para os clientes. O “quadriculado” é o piso desta região”.

E continuou: - “Também fiz um esboço dos conjuntos mesa-cadeiras que serão utilizados no restaurante”.

Considerando as informações trazidas pelo irmão mais novo, tente fazer o que se pede a seguir.

a) Coloque uma folha fina de papel sobre os esboços dos conjuntos mesa-cadeiras, cubra com um lápis os desenhos várias vezes e recorte-os de modo a ficar um conjunto mesa-cadeira em cada pedaço. Feito isso, tente posicioná-los no desenho do salão para estimar qual seria a quantidade máxima de clientes (lotação) possível para este salão.

b) De acordo com sua análise da lotação e considerando que cada lugar gere um lucro de R$ 10,00 por hora, qual o lucro esperado para uma hora de funcionamento com a lotação completa?

c) Os outros estudantes concordam com sua resposta do item anterior? Por quê?

d) Seria suficiente, ou mesmo adequado, fazer uma média das lotações obtidas por todos os estudantes e tomar essa média como sendo a real lotação do salão?

e) Que informações você identifica que poderiam ter sido trazidas pelo irmão mais novo, a fim de melhorar a estimativa da lotação?

II) Área

Entende-se como a medida de uma superfície plana.  

Unidades mais usadas: metro quadrado (m²), quilômetro quadrado (km²) e centímetro quadrado (cm²).

        1 km² = (1.000 m)² = (10³ m)² = 10⁶ m²

        1 m² = (100 cm)² = (10² cm)² = 10⁴ cm²

        1 cm² = 10^–4  m²

Área de Figuras Planas: 

Atividades:

1) Calcular a área de um quadrado cujos lados medem 0,60 m. Dê a resposta em centímetros quadrados.

2) Calcule a área de um terreno retangular cujos lados medem 1.000 m e 1.200 m. Dê a resposta em km².

3) Qual a área da bandeirinha representada pela figura abaixo?

4) Calcule a área da parte hachurada da figura abaixo:

5) Qual a área da figura abaixo?

6) Um banheiro tem dimensões 8 m x 3 m. Qual a área desse banheiro?

        (A) 24 m².

        (B) 25 m².

        (C) 26 m².

        (D) 27 m².

 

8) Mariana pretende ladrilhar o piso retangular de sua cozinha que tem 5 m x 4 m, com ladrilhos quadrados de 15 cm de lado.

a) Qual é a área de sua cozinha em metros quadrados?

b) Qual é a área de cada ladrilho?

c) De quantos ladrilhos vai precisar?

9) A figura, abaixo, mostra um terreno retangular que Manoel dividiu igualmente em três lotes retangulares. 

Qual é a medida da área desse terreno?

        (A) 100 m². 

        (B) 200 m². 

        (C) 400 m². 

        (D) 600 m².

10) Tito tem um terreno retangular cuja largura é igual a 12 metros e cuja área é igual 60 m². Quantos metros de cerca Tito deve gastar, no mínimo, para cercar o seu terreno?

        (A) 5 m        

        (B) 20 m                      

        (C) 34 m        

        (D) 48 m

11) Um pequeno terreno ABCDEF, com a forma mostrada na figura, possui área 23 m².

Para cercar esse terreno com cinco fios de arame farpado, o proprietário adquiriu 3 rolos de arame com 30 m cada um. Dessa forma:

     (A) O proprietário comprou um rolo a mais que o necessário para fazer a cerca.

           (B) O proprietário precisa comprar um rolo a mais, pois precisa de mais 15 m para completar a cerca.

           (C) O proprietário precisa comprar um rolo a mais, pois precisa de mais 25 m para completar a cerca.

           (D) O proprietário precisa comprar dois rolos a mais, pois precisa de mais 60 m para completar a cerca.

12) O lado de cada quadrado da malha quadriculada, abaixo, mede 1 cm.

A área da figura sombreada mede:

        (A) 20 cm².  

        (B) 23 cm².    

        (C) 25 cm².

        (D) 27 cm².

13) O menor país do mundo em extensão é o Vaticano, com uma área de 0,4 km². Se o território do Vaticano tivesse a forma de um quadrado, então a medida de seus lados estariam entre:

          (A) 200 m e 201 m.

          (B) 220 m e 221 m. 

          (C) 401 m e 402 m.

          (D) 632 m e 633 m.

14) Os catetos de um triângulo retângulo medem 15cm e 20cm. O perímetro e a área desse triângulo, respectivamente, são:

      (A) 60 cm e 300 cm²

      (B) 50 cm e 250 cm²

     (C) 45 cm e 350 cm²

     (D) 90 cm e 200 cm²

Outras Unidades de Medidas:

III) Massa     

 Entende-se como quantidade de matéria de um corpo.

A unidade padrão de medida de massa é o quilograma (kg). Os múltiplos e submúltiplos do quilograma mais usado é: o grama(g), o miligrama(mg) e a tonelada (t).

Assim, temos: 

        1 t = 1.000kg = 10³ kg                    

        1 kg = 1.000 g = 10³ g                                 

        1 g = 0,001 kg = 10^-3 kg                                  

        1 mg = 0,001 g = 10^-3 g                                        

        1 mg = 10^-6 kg

 

 

VI) Intervalo de Tempo

Entende-se a duração de uma atividade que nos dá ideia de presente, passado e futuro ou período no qual um evento ocorre.

A unidade padrão de tempo é o segundo (s).

O segundo, admite, entre outros, os seguintes múltiplos: minuto (min), hora (h) e dia.

Assim, temos: 

        1 min = 60 s                               

        1 h = 60 min = 3.600 s                                  

        1 dia = 24 h = 86.400 s

Atividades:

1) Um avião tem capacidade para quatrocentos passageiros. Cada pessoa tem, em média, massa de 70kg e pode levar 20kg de bagagem.  Quantas toneladas esse avião tem capacidade para carregar?

 

2) Dona Margarida precisa descobrir a massa de um único feijão. Usando uma balança, descobriu que a massa de mil feijões era de 0,47 kg. Desse modo, Dona Margarida determinou a massa de um feijão em quantos gramas?

 

3) Em uma eleição, cinco eleitores demoram para votar, respectivamente: 1min 28s, 2min 50s, 1min 16s e 1min 42s. Qual o total de tempo gasto por estes eleitores?

 

4) Um ônibus partiu de seu ponto de embarque às 14h34min, retornando ao mesmo ponto como desembarque às 18h39min. Determine o intervalo de tempo da viagem desse ônibus?

5) Numa sacola estão 3 kg de batata, 1 kg de feijão, 400 g de queijo, 250 g de azeitona e 2 kg de arroz. Qual é o peso total dos alimentos?

        (A) 1,9 kg    

        (B) 3,85 kg    

        (C) 4,75 kg     

        (D) 6,65 kg

 

6) Se 1kg de carne custa 15 reais, quanto pagarei por  3.200 g?

        (A) R$ 30,00

        (B) R$ 32,00

        (C) R$ 34,00

        (D) R$ 48,00

 

7) Um botijão de cozinha contém 13 kg de gás. Em média, é consumido, por dia, 500 g. Depois de quantos dias o botijão estará vazio?

        (A) 25 dias

        (B) 26 dias

        (C) 28 dias

        (D) 30 dias

 

8) Se 2,5 kg de queijo custaram R$ 50,00, qual o preço do quilograma desse queijo?

        (A) R$ 20,00

        (B) R$ 15,00

        (C) R$ 25,00

        (D) R$ 10,00

Desafio Interessante:

Muitas pessoas projetam e constroem as próprias casas, o que pode fazer com que a tarefa pareça mais simples do que realmente é. Por exemplo, um erro muito comum envolve desconsiderar o peso de objetos que serão colocados após a construção.

Seu João é uma dessas pessoas que gostam de “botar a mão na massa” e, a pedido de sua esposa, que adora jardinagem, decidiu projetar uma varanda para o seu quarto. A área útil terá o formato de um retângulo de dimensões 3 m por 1,5 m; seu João fez os cálculos necessários e saiu para comprar os materiais. Antes de sair, porém, foi interpelado por sua esposa:

— João, tem certeza de que a varanda aguenta o peso dos vasos? Terra vegetal pesa muito!

— Maria, meu amor, eu sei o que estou fazendo. Com o meu projeto, 5 pessoas de 70 kg, como você, poderiam ficar na varanda ao mesmo tempo e mesmo assim ela não cederia.

E seu João foi às compras, enquanto dona Maria, que sempre gostou de Matemática, decidiu fazer algumas contas para ver se seu marido estava correto. Ela quer colocar na varanda duas jardineiras completamente cheias, cada uma pesando 10 kg e com capacidade para 75 litros de terra vegetal. Devido aos anos de jardinagem, dona Maria sabe que 1 litro de terra vegetal corresponde a 1,5 kg. Considerando que o cenário descrito por seu João representa o limite de carga da varanda:

 a) Qual a área disponível para a varanda?

b) Qual o ‘peso’ total das duas jardineiras cheias de terra vegetal?

c) Quantas pessoas de 70 kg poderão está na varanda juntamente com as duas jardineiras cheias de terra vegetal, respeitando o limite máximo de peso que seu João havia estipulado?

Aprofunde-se: https://convertlive.com/pt/c/converter/comprimento

                    https://convertlive.com/pt/c/converter/%C3%A1rea

“Em alguma medida, nossa vida dá-se sob a ciência dos números: por ela sabemos as horas, acompanhamos o curso dos meses, sabemos quando retorna cada época do ano. Pelo número aprendemos a evitar enganos. Suprimido o número de todas as coisas, tudo perece. Se se tira o cômputo dos tempos, tudo ficará envolto na cega ignorância e o homem não se pode diferenciar dos animais, que ignoram os procedimentos de cálculo."

                                                                                                                     Santo Isidoro (560 – 636 d.C.)