Parábola é o conjunto dos pontos de um plano, tais que da distância a um ponto
fixo desse plano (foco) é sempre à
distância a uma reta fixa (diretriz).
 |
| cinta de metal, perfurada para receber ligaduras de fibra, com as quais eram | amarrados os dentes. |
Já vimos a utilidade da parábola como representação de uma função
quadrática, porém, há muitas aplicações para essa curva. Por exemplo, o
cirurgião dentista estadunidense Edward Hartley Angle (1855-1930), conhecido
internacionalmente mentor da Ortodontia moderna, descreveu como forma ideal do
arco dentário a forma de uma parábola. Posteriormente, outros grandes
nomes da ortodontia, como Emil Herbst, adotam também essa forma como a ideal.
Também sabemos que o lançamento oblíquo de uma bola, de um projétil ou de
uma pedra pode descrever uma parábola.
Seja, em um plano α, uma reta d e um ponto F não pertencente a d. O conjunto de pontos de α equidistantes de d e de F é denominado de parábola.
Na figura podemos notar as distâncias:
d(P, d)
= d(P, F)
d(Q, d)
= d(Q, F)
d(R, d) = d(R, F)
d(V,
d) = d(V, F)
Elementos de uma parábola:
Foco: F (ponto fixo
da definição);
Reta
diretriz: d (reta fixa da
definição);
Vértice: V (ponto
médio de FB; FB perpendicular a d e B pertencente a d);
Eixo de simetria: a reta que passa por V e F (reta VF);
Parâmetro: p > 0,
distância de F a B, d(F, B) = d(F, d) = p;
Sendo p o parâmetro da parábola, BF
= p, BV = p/2 e VF = p/2.
Aplicando a definição dada, podemos obter a equação de uma parábola com
vértice na origem do referencial e foco em um dos eixos coordenados.
Exemplo: Qual é a equação da parábola que tem diretriz de equação x = –2 e foco F(2, 0)?
Por definição: d(P, F) = d(P, d). Assim, temos:
Elevando ao quadrado os dois membros da igualdade, chegamos a:
(x – 2)2
+ y2 = (x + 2)2
x2
– 4x + 4 + y2 = x2 + 4x + 4.
Portanto, a equação dessa parábola é:
y2
= 8x.
Podemos desenhar de quatro maneiras uma parábola com vértice na origem e
foco dos eixos coordenados. Observe nas figuras abaixo cada parábola resulta
numa equação diferente:
Exemplos:
1) Achar a equação da parábola de vértice na origem e foco F(0, 4) usando uma das fórmulas acima.
Esboçando o gráfico da parábola, observamos que sua equação será x2 = 2py:
Mas p/2 = 4. Assim, p = 8.
Portanto, x2 = 2 ∙ 8y, isto é, x2 = 16y.
2) Um dos cabos de sustentação de uma ponto de 160 m de comprimento é um arco de parábola preso a pilares verticais de 20 m de altura. O vértice V da parábola é o ponto médio do segmento de reta que liga as bases A e B dos pilares, como mostra a figura.
Entre os pilares há seis cabos que sustentam o piso da ponte, de modo que a extremidade inferior de cada um dos cabos e o vértice V da parábola dividem o segmento AB em oito segmentos congruentes entre si. Calcular o comprimento de cada um dos dois cabos menores.
Solução:
Em um sistema de coordenadas cartesianas, podemos representar a situação do seguinte modo:
Como podemos observar a equação da parábola que tem vértice na origem e foco
num dos eixos coordenados é bem simples. Basta aplicar a definição de parábola
para encontra-la.
Outro tipo de problema pede o estudo da parábola a partir da equação,
dada em uma das quatro apresentações: y2 = 2px; y2= –2px; x2 = 2py; x2 = –2py;
que revelam uma parábola com vértice na origem e foco num dos eixos. Neste caso, descobrimos o valor de p por identificação.
Agora, caso o vértice não esteja na origem, as coordenadas do foco são:
sendo V(x0, y0).
Daí, análogo aos casos anteriores, teremos quatro casos:
1º caso:
Diretriz paralela ao eixo y e F à direita da diretriz:
(y – y0)2 = 2p∙(x – x0)
F(x0 + p/2, y0)
(d): x = x0 – p/2
2º caso: Diretriz paralela ao eixo y e
F à esquerda da diretriz:
(y – y0)2 = –2p∙(x – x0)
F(x0 – p/2, y0)
(d): x = x0 + p/2
3º caso: Diretriz paralela ao eixo x e F acima da diretriz:
(x – x0)2 = 2p∙(y – y0)
F(x0, y0 + p/2)
(d): y = y0 – p/2
4º caso: Diretriz paralela ao eixo x e F abaixo da
diretriz:
(x – x0)2 = –2p∙(y – y0)
F(x0, y0 – p/2)
(d): y = y0 + p/2
Somente os 3º e 4º casos podem definir uma função quadrática.
Exemplo: Dada a representação da parábola de equação (y + 3)² = 4∙(x – 1) no gráfico abaixo:
b) A coordenada do foco dessa parábola é da forma F(x0 + p/2, y0), para isso, é preciso termos o valor do parâmetro que é dado pela equação:
2p = 4
p = 2
p/2 = 1.
Daí, F(1 + 1, –3), logo F(2, –3).
c) A reta diretriz tem a forma (d): x = x0 – p/2, daí a reta diretriz dessa equação é:
x = 1 – 1
x = 0.
Nesse caso, a reta diretriz é o próprio eixo y.
d) Fazendo algebricamente o cálculo equação na forma estendida, temos:
(y + 3)² = 4∙(x – 1)
y² + 6y + 9 = 4x – 4
y² + 6y – 4x + 13 = 0.
E observamos que essa forma algébrica não assume a forma de uma função quadrática y = ax² + bx +c, logo essa parábola não representa uma função quadrática.
Atividades:
1) Uma ponte suspensa tem 30 m de largura. As colunas que a suspendem têm 10 m de altura, como na figura abaixo:
O cabo de sustentação tem a forma parabólica, sendo que o seu ponto mais
baixo está a 6 m da pista. Qual é o comprimento do suporte que está a 5 m do
centro da ponte?
2) O cabo de uma ponte suspensa tem a forma de uma parábola. As torres que suportam os cabos estão a 120 m uma da outra, como se vê na figura abaixo:
O cabo passa por dois apoios que estão a 20 m do piso e seu ponto mais
baixo está no nível do chão. Ache o comprimento dos tirantes verticais que vão
do cabo à ponte a intervalos de 20 m, do centro até os apoios.
3) Um arco parabólico tem 3 m de altura e 4 m de largura da base. O vértice da parábola está no topo do arco.
A que altura, sobre a base, a parábola tem 2 m de largura?
4) Alguns telescópios usam espelhos parabólicos, pois essa forma geométrica reflete a luz que entra para um único ponto, chamado foco. O gráfico de y = x2, por exemplo, tem a forma de uma parábola.
A
luz que vem verticalmente, de cima para baixo (paralelamente ao eixo y), encontra a parábola e é refletida
segundo a lei de que o ângulo de incidência é igual ao ângulo de reflexão. Essa
lei implica que os raios de luz verticais, encontrando a parábola no ponto (a, a2),
serão refletidos na direção da reta
4ay + (1 – 4a2)x = a.
Sendo
assim, calcule o ponto em que os raios de luz verticais refletidos em (1,1) e
(2,4) se encontrarão.
5) Ao dirigir o jato de água de uma mangueira obliquamente para cima, Pedro observou que a trajetória percorrida pela água é parabólica. O bico B da mangueira está a 1 m de altura em relação ao solo plano e horizontal, e a água atinge a altura máxima de 2 m, em relação ao solo, em um ponto V sobre uma reta vertical que dista 1,6 m de B.
a) A que altura, em relação ao solo, passa a diretriz dessa parábola?
b) A que altura, em relação ao solo, está o foco dessa parábola ?
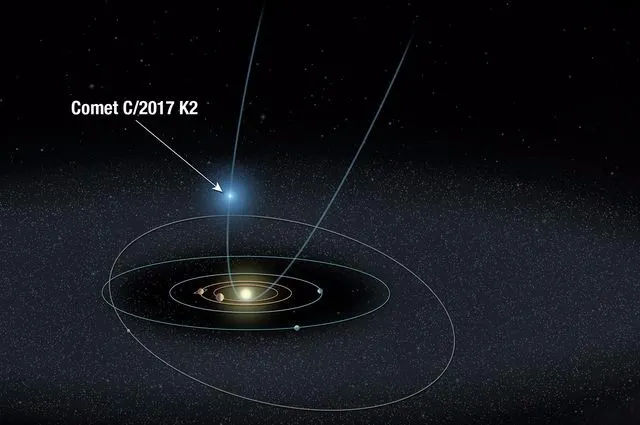
6) A
órbita de um cometa é uma parábola cujo foco F é o Sol. Para o estudo do movimento
desse cometa, um astrônomo fixou um sistema cartesiano ortogonal xOy no plano dessa órbita, adotando
nos eixos uma unidade de comprimento u, conveniente para grandes distâncias.
Em relação a esse sistema, a
trajetória parabólica descrita pelo cometa tinha o eixo Oy como eixo de simetria e a
concavidade voltada para o sentido positivo desse
eixo, com o Sol no ponto F (0,
7). Com isso, o cientista calculou que, quando o cometa passou pelo
ponto P(6, 7), sua distância ao Sol era 6 u.
(Nota: A órbita de um cometa pode ser
elíptica, parabólica ou hiperbólica. Quando a órbita é elíptica, o cometa é
periódico; ou seja, ele entra periodicamente no Sistema Solar. Quando a órbita
é parabólica ou hiperbólica, o cometa não é periódico, passando uma única vez
pelo Sistema Solar.)
Forma canônica da função quadrática
Suponha
que conheçamos as coordenadas (m, k) do vértice de uma parábola, bem como o coeficiente a, que fornece sua concavidade e
abertura.
Nesse
caso, é fácil determinar a expressão da função quadrática f(x) correspondente, bem como traçar o seu gráfico, bastando para
isso que apliquemos sobre a função q(x) =
x2 algumas das transformações apresentadas abaixo:
Em
linhas gerais, essa estratégia de obtenção de uma função quadrática pode ser
dividida nos seguintes passos:
1. Escolha
ou estique a função q(x) = x2
de forma a obter h(x) = ax2.
Supondo que a > 0, o gráfico de h
será similar à curva tracejada mostrada na Figura acima. Por outro lado, se a
< 0, o gráfico de h incluirá uma
reflexão da parábola em relação ao eixo-x.
2.
Desloque o gráfico da função h por m unidades na horizontal para obter g(x) = a∙(x
– m)2. Supondo que m
seja um valor positivo, o deslocamento será para a direita e o gráfico de g equivalerá à curva verde da Figura abaixo,
na qual a coordenada-x do vértice é m. Já para m < 0, haverá um deslocamento para a esquerda.
3.
Desloque o gráfico de g por k unidades na vertical para obter f(x) = a(x − m)2 + k.
No
caso em que k > 0, haverá um
deslocamento para cima e o gráfico de f
será equivalente à curva azul apresentada na acima.
Já
se k < 0, a parábola será
deslocada para baixo.
(a)
Deslocamento de m unidades na
horizontal
(b)
Deslocamento de k unidades na
vertical
Esse
procedimento para a obtenção de uma parábola com abertura a e vértice (m, k) sugere que toda função quadrática
pode ser apresentada na forma canônica
f(x) = a(x − m)2 + k.
(Forma
canônica) Para mostrar que é sempre possível converter uma função quadrática f(x) = ax2 + bx + c para a
forma canônica, e vice-versa, basta estabelecer uma relação única entre os
coeficientes de uma e outra forma.
Essa
relação pode ser obtida expandindo a forma canônica: f(x) = a(x − m)2 + k
f(x) = a(x2 − 2mx + m2) + k
f(x) = ax²− 2amx + am2 + k
Comparando
essa expressão de f(x) com a forma
usual
f(x) = ax2+bx+c, concluímos
que o coeficiente a que aparece nas duas formas é o mesmo.
Além
disso, b = −2am e c = am2 + k.
Assim,
percebemos que é fácil determinar os coeficientes b e c a partir de a e das coordenadas do vértice da
parábola.
Vejamos,
agora, como obter m e k a partir de a, b e c.
Como
b = −2am, temos m = −b/2a.
Da
mesma forma, como c = am2 + k,
podemos escrever:
O
quadro a seguir resume as fórmulas de conversão entre os dois principais
formatos de uma função quadrática.
Embora
não seja muito empregada, a forma canônica é útil quando se quer escrever uma
função quadrática (ou traçar seu gráfico) a partir das coordenadas do vértice,
como mostra o problema abaixo.
De outra forma é possível escrever V(m, k) como V (x0, y0) e até mesmo V(xv, yv).
Exemplo: Encontre a função quadrática
cujo gráfico tem vértice em (−3, 4) e que passa pelo ponto (−5, −4). Em
seguida, trace o gráfico da função.
f(x) = a(x − (−3))2 + 4 ⇒ f(x) = a(x + 3)2 + 4.
Usando, agora, o fato de que a parábola passa pelo ponto (−5, − 4), escrevemos f(−5) = −4, de
modo que
−4 = a(−5 + 3)2
+ 4
−4 = a(−2)2
+ 4
−8 = 4a
−2 = a.
Logo,
a função quadrática
é f(x)
= −2(x
+ 3)2 + 4.
Para
traçar o gráfico de f(x), cujo vértice é (−3, 4), deslocamos a parábola y = −2x2 três unidades para a
esquerda e quatro unidades para cima, como mostra o gráfico abaixo:
Atividades:
1)
Determine a função quadrática que satisfaz cada uma das condições abaixo.
a)
Tem vértice em (1, −2) e passa pelo ponto (2, 3).
b)
Tem vértice em (3, 4) e cruza o eixo-y na
ordenada −5.
2) Num projeto arquitetônico precisa-se fazer em uma construção um arco parabólico que tenham 9 m de altura e 6 m de largura na base. O vértice da parábola está no topo do arco.
a) Qual a equação reduzida da parábola nesse projeto?
b) Determine a equação da parábola na forma y = ax² + bx + c.
c) A que altura, sobre a base, o arco terá 4 m de largura?
d) A que altura, sobre a base, o arco terá 2 m de largura?
3) Um arquiteto precisa fazer em uma construção um arco parabólico que tenham 4 m de altura e 6 m de largura na base. O vértice da parábola está no topo do arco.
a) A que altura, sobre a base, o arco terá 4 m de largura?
b) Faça o desenho desse arco.
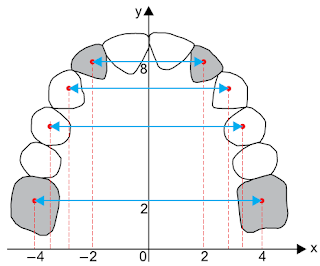
4) A figura representa o desenho
da arcada dentária de um animal, feito no plano cartesiano ortogonal em escala
linear.
Sabendo que as posições dos
centros dos dentes destacados em cinza nessa arcada são modeladas nesse plano
por meio da função quadrática y = ax2 +
b, então a + b é igual a:
(A) 8,5.
(B) 9,2.
(C) 9,5.
(D) 10,2.
(E) 9,0.
5) Os cabos de sustentação de uma ponte pênsil com carga uniformemente distribuída tomam forma de uma parábola cujo vértice está no tabuleiro da ponte. As torres de suporte têm 20 metros de altura sobre o tabuleiro e distam 160 metros entre si. Supondo o sistema de coordenadas cartesianas com eixo x no tabuleiro e eixo y sendo eixo de simetria da parábola, o comprimento de um elemento de sustentação vertical situado a 40 metros do centro da ponte é:
(A) 10 m
(B) 4 m
(C) 3,2 m
(D) 5 m
(E) 0,5 m
6) Uma ponte suspensa de 400 m de comprimento é sustentada por um cabo principal parabólico. O cabo principal está 100 m acima da ponte nos extremos e 4 m acima da ponte em seu centro. Calcule o comprimento dos cabos de sustentação que são colocados a intervalos de 50 m ao longo da ponte. (Sugestão: Utilize o sistema de coordenadas retangulares em que a ponte é o eixo x e a origem está no meio da ponte).
Aprofunde-se:




























Nenhum comentário:
Postar um comentário