Sejam
dados os coeficientes reais a, b e c,
com a ≠ 0. A função definida por f(x) =
ax2 + bx + c é denominada função
quadrática.
As funções quadráticas têm
aplicações em áreas variadas, como a física, a economia, a engenharia, a
biologia e a geografia.
O problema abaixo mostra o
emprego de uma função quadrática à descrição da trajetória de uma bola.
Problema 1. Um golfista dá uma tacada que faz sua bola descrever
uma trajetória na qual a altura, em metros, é dada pela função f(x) = −0,008x2 + x, em que x é a distância horizontal da bola, em
metros, medida a partir de sua posição antes da tacada.
Quando a bola está a uma
distância horizontal x do ponto de
partida, sua altura é f(x).
a) Determine a altura da bola
quando ela está a uma distância horizontal de 40 m de seu ponto de partida.
b) Com base em uma tabela de
pontos, trace a trajetória da bola no plano Cartesiano.
c) Determine a que distância
do ponto de partida a bola cai no chão.
Solução:
a) A altura da bola quando ela
está a uma distância horizontal de 50 m de sua posição original é dada por
f(40) = −0,008 ⋅
402 + 40 = 27,2.
Logo, a bola está a uma altura de 27,2 m.
b) A Tabela abaixo fornece uma
lista de pares ordenados obtidos a partir da definição de f.
Com base nesses pontos, traçamos o gráfico abaixo, que mostra a trajetória descrita pela bola:
c) Observando o gráfico, concluímos
que a bola toca o solo a cerca de 125 metros de seu ponto de partida. Para
determinar com exatidão a coordenada horizontal desse ponto, basta lembrar que
dizer que a bola está sobre o solo é o mesmo que afirmar que sua altura é zero.
Assim, temos f(x) = 0, ou seja,
−0,008x2 + x = 0
x(−0,008x + 1) = 0.
Assim temos, as raízes dessa equação devem
satisfazer
x = 0 ou −0,008x + 1 = 0.
Nesse último
caso, temos
−0,008x + 1 = 0
−0,008x = −1
x = −1 / −0,008
x = 125.
A curva mostrada no trecho entre x = 125 e x = 140, no qual os valores de f(x) são negativos. Esse trecho foi usado apenas para completar a trajetória até o ponto de queda, não implicando que, na prática, a bola tenha tido uma altura negativa, o que só aconteceria se ela fosse enterrada no solo.
É importante notar que uma função quadrática pode ser fornecida em outro formato que não aquele apresentado no quadro acima, como mostram os exemplos a seguir.
Problema 2: Converta as funções abaixo ao formato f(x) = ax2 + bx + c.
a) f(x) = 2(x − 1)(x + 3)
b) f(x) = −3(x − 4)2
+ 6
Solução.
a) Aplicando a propriedade distributiva, podemos escrever
2(x − 1)(x +
3) = 2(x2 − x + 3x − 3) = 2x2 + 4x − 6.
Logo, f(x) = 2x2 + 4x − 6.
b) Usando a regra do quadrado da soma (ou a propriedade distributiva
mais uma vez), obtemos:
−3(x − 4)2 + 6 = −3(x2 − 8x + 16) + 6 = −3x2
+ 24x − 48 + 6 = −3x2 + 24x − 42.
Assim, f(x) = −3x2 + 24x − 42.
Gráfico das funções quadráticas
O gráfico
de uma função quadrática tem um formato característico – similar a uma letra
“U” mais aberta –, e é chamado parábola.
A Figura abaixo mostra duas
parábolas típicas.
Observando as curvas dos
gráficos, notamos que a função quadrática tem um ponto de mínimo ou um ponto
de máximo local. A esse ponto especial da parábola damos o nome de vértice.
Além disso, toda parábola é
simétrica a uma reta vertical que passa por seu vértice. Essa reta vertical é
denominada eixo de simetria.
Outra característica
importante de parábola é a sua concavidade,
que é a lado para o qual a curva se abre. Na primeira curva mostra uma parábola
com concavidade para cima, enquanto a
segunda curva mostra uma parábola com concavidade
para baixo.
Note que há uma relação entre
a concavidade e o sinal do coeficiente a. Se a > 0, a parábola tem concavidade
para cima. Por outro lado, a concavidade
é para baixo se a < 0.
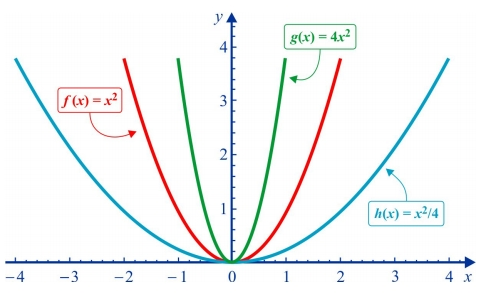
O parâmetro a também controla a abertura da
parábola. Quanto maior for o valor absoluto desse parâmetro, menor será a
abertura, e vice-versa, como ilustra o gráfico abaixo:
Por sua vez, o coeficiente c da função quadrática determina o intercepto-y da parábola, pois, tomando x = 0, temos:
f(0) = a ⋅
02 + b ⋅
0 + c = c.
Já os interceptos-x da parábola correspondem às raízes da equação f(x) = 0, que é equivalente à equação
quadrática ax2 + bx + c = 0.
Resolução de Equação de 2º grau ou zero da função quadrática
A ideia principal do método
para resolver uma equação do tipo ax2
+ bx + c = 0, com a ≠ 0, é essa:
ü Se
ax2 + bx + c for um
quadrado perfeito, podemos fatorá-lo na forma (d + e)2 ou (d –
e)2, cuja resolução é simples. Acompanhe a resolução de 16x2 + 8x + 1 = 16.
Fatoramos: 16x2 + 8x + 1 em (4x + 1)2, escrevemos (4x + 1)2 = 16
e obtemos 4x + 1 = 4 ou 4x + 1 = –4.
Resolvendo as equações acima,
temos: x = 3/4 ou x = –5/4.
S = {−5/4, 3/4}.
ü Se
o trinômio não for um quadrado perfeito, para resolver a equação proposta
devemos completar um quadrado perfeito a partir da expressão dada. Acompanhe o
quadro abaixo:
Com isso, obtemos a fórmula
geral de resolução, na qual b2
– 4ac é o discriminante, também
representado pela letra grega maiúscula ∆ (“delta”).
Essa expressão é conhecida como fórmula de Bhaskara, em homenagem ao matemático indiano Bhaskara Akaria (1114-1185).
Exemplo: Dada a função quadrática f(x) = 2x2 − 5x − 3, determine os interceptos de seu
gráfico com os eixos coordenados.
Solução:
• O intercepto-y da parábola é dado pelo coeficiente c, cujo valor é −3.
• Para obter os interceptos-x, devemos resolver a
equação 2x2 − 5x − 3 = 0.
Nesse caso, o discriminante vale
∆ = b2 − 4ac = (−5)2
− 4 ⋅
2 ⋅
(−3) = 25 + 24 = 49.
Como ∆ > 0, sabemos que o
gráfico intercepta o eixo-x em dois
pontos.
Recorrendo, então, à fórmula
de Bhaskara, obtemos:
Logo, os interceptos são:
Podemos analisar acerca do
papel do discriminante:
∆ = b2 − 4ac
do polinômio quadrático, numa função quadrática e podemos dizer que a parábola:
• intercepta o eixo-x em dois pontos se
∆ > 0;
• intercepta o eixo-x em um ponto se ∆ = 0;
• não
intercepta o eixo-x se ∆ < 0.
Atividades:
1) Um terreno, que tem a forma
de um quadrado, foi reduzido da maneira indicada na figura abaixo, para dar
lugar a uma calçada com 2m de largura. Ao final, sua área passou a ser de
484m². Qual era a medida do lado do terreno original?
2) Resolva as equações abaixo:
a) x2 = 4
b) (2x – 3)2 = 25
c) 25x2
+ 90x + 81 =0
d) x2 – 2x – 15 = 0
e) 2x2 + 3x + 1 = 0
3) O produto entre dois números naturais consecutivos é 156. A soma desses dois números é:
(B) 24 metros.
(C) 26 metros.
(D) 28 metros.
4) Antônio, com 20m de cerca, construiu
um cercado retangular de 32m² de área, utilizando seu muro como um dos lados.
Quais as medidas dos lados desse cercado retangular?
5)
6) Para presentear os colegas no natal, Ana comprou alguns exemplares de um livro por R$ 540,00. Por ter obtido um desconto de R$ 15,00 no preço de cada exemplar do livro, ela conseguiu comprar 3 exemplares a mais do que previra originalmente. Com o desconto concedido, quantos exemplares desse livro Ana comprou?
7) O dono da marcenaria, que
fabrica certo tipo de armário, verificou que o número N de armários que ele pode fabricar por mês depende do número x de funcionários trabalhando na
marcenaria e que essa dependência é dada pela igualdade N = x2 + 2x. Qual é o número de funcionários necessários
para a marcenaria fabricar 168 armários em um mês?
8) Uma pessoa distribui 240
balas para um certo número de crianças. Se cada criança receber uma bala a
menos, o número de balas que cada criança vai receber será igual ao número de crianças.
Qual é o número de crianças?
9) Defina uma função f(x)
que forneça a área da região destacada na figura, lembrando que a área de um
retângulo de lados b e h é bh.
10) Dada a função
f(x) = x2 − 3x:
a) determine algebricamente os
pontos nos quais f(x) = 0;
b) determine algebricamente os
pontos nos quais f(x) = −2; c) esboce
o gráfico da função no plano coordenado, indicando os pontos que você obteve no
item (b);
d) determine graficamente as
soluções da inequação f(x) ≥ −2.
11) Dada a função f(x) = 5x − 2x2:
a) determine algebricamente os
pontos nos quais f(x) = 0;
b) determine algebricamente os
pontos nos quais f(x) = 2;
c) esboce o gráfico da função
no plano coordenado, indique os pontos que você obteve no item (b);
d) determine graficamente as
soluções da inequação f(x) ≥ 2.
11) Dada a função f(x) = −2x2 + 9x:
a) determine algebricamente os
pontos nos quais f(x) = 0;
b) determine algebricamente as
soluções da inequação f(x) ≥ 9;
c) determine algebricamente o
ponto de mínimo ou máximo de f;
d) esboce o gráfico da função
no plano coordenado.
12) Dada a função f(x) = −3x2 + 15x:
a) determine algebricamente os
pontos nos quais f(x) = 0;
b) determine algebricamente as
soluções da inequação f(x) ≥ 12;
c) determine algebricamente o
ponto de mínimo ou máximo de f;
d) esboce o gráfico da função
no plano coordenado.
13) Dada a função f(x) = 15x2
+ x – 2:
a) determine algebricamente os
pontos nos quais f(x) = 0;
b) determine algebricamente as
soluções da inequação f(x) ≤ −2;
c) determine algebricamente o
ponto de mínimo ou máximo de f.
14) Esboce o gráfico e determine
o ponto de mínimo ou máximo de cada função.
a) f(x) =
(x − 1)(x + 2)
b) f(x) =
(−3 − x)(x + 3)
c) f(x) =
x2 − 3x + 4
d) f(x) =
−2x2 + 3x + 2
e) f(x) =
4x + x2
f) f(x) =
−x2 − 4
g) f(x) =
(x − 4)(x + 1)
15) Um grupo de amigos, numa
excursão, aluga uma van por 342
reais. Findo o passeio, três deles estavam sem dinheiro e os outros tiveram que
completar o total, pagando cada um deles 19 reais a mais. Quantos eram os
amigos?
Aprofunde-se:













Nenhum comentário:
Postar um comentário