Equação da Reta

Algumas roupas são apropriadas para determinadas ocasiões. No laser e no trabalho, por exemplo, os trajes são diferentes.

Podemos imaginar a mesma situação em Matemática. As equações da reta variam de acordo com as circunstâncias, embora a reta continue sendo a mesma.

 

Seja dada uma equação linear em duas variáveis y = ax + b, em que a e b são constantes reais. A representação dessa equação no plano Cartesiano é dada por uma reta. 

Já foi estudado que a inclinação a da reta que passa por (x₁,y₁) e (x₂,y₂), com x₁ ≠ x₂, é dada por:

Sabe-se também que se conhecermos a inclinação a de uma reta e o ponto (0, b) no qual ela intercepta o eixo y, podemos escrever sua equação na forma y = ax + b.

Por exemplo, a equação da reta que passa por (0, 1) e tem inclinação 2 é y = 2x + 1.

De modo geral, chamamos a equação y = ax + b de Equação Reduzida da Reta.

 

Equação da reta a partir da inclinação e de um ponto

Suponha que conheçamos um ponto (x₁, y₁) pelo qual passa uma reta. Suponha, também, que (x, y) seja um ponto qualquer dessa mesma reta, com x ≠ x₁. Nesse caso, a inclinação da reta é definida como:

 .

Multiplicando, agora, os dois lados por (x − x₁), obtemos: 

a∙(x − x₁) = y  − y₁.

 

 Note que essa equação é satisfeita por todos os pontos (x, y) da reta, incluindo o ponto (x₁, y₁). Assim, podemos dizer que essa é uma forma alternativa de se apresentar a equação da reta. De fato, essa forma é bastante adequada quando conhecemos a inclinação e um ponto pelo qual a reta passa.

 

E de modo geral, a equação da reta da qual se conhece a inclinação a e um ponto A(x₁, y₁) é:

y − y₁  = a∙(x − x₁).

 

Exemplo: Obter a equação da reta s, que passa pelo ponto A(−2, 3) e tem inclinação  −4.

Substituindo em y  − y₁  = a∙(x − x₁) =, os dados temos:

y – 3 = −4∙(x –(−2))

y – 3 = −4∙(x + 2)

y – 3 = −4x – 8

y = −4x – 8 + 3

y = −4x – 5

 Logo, a equação reduzida da reta é dada por y = −4x – 5.

 

Equação da reta que passa por dois pontos conhecidos 

Existe apenas uma reta que passa por dois pontos distintos (x₁, y₁) e (x₂, y₂) do plano coordenado. Para determinar a equação dessa reta devemos, em primeiro lugar, calcular sua inclinação através da fórmula

 .

Em seguida, escrevemos a equação usando um dos pontos dados, como descrito no quadro acima. O exemplo a seguir ilustra essa estratégia de obtenção da equação.

 

Exemplo: Determinar a equação da reta r que passa pelos pontos (x₁, y₁) = (2, 1) e (x₂, y₂) = (3, −1):

Calculamos, primeiramente, sua inclinação:

Usando, agora, o ponto (2, 1), escrevemos:

y − 1 = −2∙(x − 2).

E fazemos:

y − 1 = −2x − 2⋅ (−2) 

 y = −2x + 4 + 1 

 y = −2x + 5.

 

Observe que o mesmo resultado seria obtido se usássemos o ponto (x₂,y₂) = (3, −1) para escrever a equação, em lugar de (x₁,y₁) = (2,1). Nesse caso, teríamos:

 y − (−1) = −2∙(x − 3) 

 y + 1 = −2∙(x − 3).

Apesar de essa equação parecer diferente da que foi obtida acima, um pouco de álgebra nos mostra que o resultado é o mesmo:

y + 1 = −2x − 2 ⋅ (−3) 

 y = −2x + 6 − 1 

 y = −2x + 5.

 

 

Retas horizontais e retas verticais

Em uma reta horizontal, todos os pontos têm a mesma coordenada y, ou seja, tomando dois pontos distintos, digamos (x₁, y₁) e (x₂, y₂), temos y₁ = y₂. Sendo assim, a inclinação da reta é:

Logo, a equação da reta pode ser escrita simplesmente como y = y₁.

 

Por outro lado, em uma reta vertical, todos os pontos têm a mesma coordenada x. Nesse caso, enfrentaríamos um sério problema se quiséssemos calcular a, pois, como x₁ = x₂, teríamos:

  

Como a divisão por zero não está definida, não é possível escrever a equação de uma reta vertical na forma y = ax + b.

De fato, a equação desse tipo de reta é simplesmente x = x₁.

Assim, de modo geral:

a) A equação da reta horizontal que passa pelo ponto é y = y₁.

b) A equação da reta vertical que passa pelo ponto é x = x₁.

Exemplo: A Figura mostra a reta horizontal e a reta vertical que passam pelo ponto (2, 1).

Nesse caso:

• a equação da reta horizontal é y = 1, 
• enquanto a reta vertical é descrita pela equação x = 2.

 

Construindo o gráfico das retas

Construir o gráfico das retas r e s de equações abaixo apresentadas:

r: y = 2x – 8

s: y = –3x + 6

Basta marcar na reta o coeficiente linear apresentado na equação, onde o gráfico corta o eixo y e calcular y = 0, onde o gráfico corta o eixo x. Finalmente, unir os dois pontos com uma reta passando entre eles.

Na reta r temos –8 que corta o eixo y e fazendo 2x – 8 = 0, temos x = 4, onde o gráfico corta o eixo x.

Na reta s temos 6 que corta o eixo y e fazendo –3x + 6 = 0, temos x = 2, onde o gráfico corta o eixo x. 

 

Exemplos:

1) Verificar se o ponto (2, –4) pertence a reta r e se pertence a reta s.

Basta substituir um dos valores das coordenadas na equação da reta e verificar se encontra a outra coordenada correspondente do ponto.

Em r: y = 2x – 8 substitui a abscissa 2 na equação:

y = 2 ∙ 2 – 8 = 4 – 8 = –4.

Como de fato foi encontrada a ordenada –4 correspondente  ao ponto dado, logo esse ponto pertence à reta r.

Agora, em s: y = –3x + 6 substitui a abscissa 2 na equação:

y = –3 ∙ 2 + 6 = –6 + 6 = 0.

Como foi encontrado um valor diferente da ordenada –4 correspondente  ao ponto dado, logo esse ponto não pertence à reta s.

Ou, de outra maneira, substituir os valores das coordenadas na equação e verificar se a igualdade é verdadeira:

a) Na equação da reta r:

–4 = 2 ∙ 2 – 8

–4 = 4 – 8

–4 = –4    (V)

A igualdade é verdadeira, logo o ponto pertence à reta r.

b) Na equação da reta s:

–4 = –3 ∙ 2 + 6

–4 = –6 + 6

–4 = 0    (F)

A igualdade é falsa, logo o ponto não pertence à reta s.

2) Verificar se o ponto (1, 3) pertence à reta r e se pertence à reta s.

Do mesmo modo que o anterior, com as coordenadas do ponto dado.

Em r: y = 2x – 8 substitui a abscissa 1 na equação:

y = 2 ∙ 1 – 8 = 2 – 8 = –6.

Como foi encontrado um valor diferente da ordenada 3 correspondente  ao ponto dado, logo esse ponto não pertence à reta r.

Agora, em s: y = –3x + 6 substitui a abscissa 5 na equação:

y = –3 ∙ 1 + 6 = –3 + 6 = 3.

Como de fato foi encontrada a ordenada 3 correspondente  ao ponto dado, logo esse ponto pertence à reta s.

Ou, de outra maneira, substituir os valores das coordenadas na equação e verificar se a igualdade é verdadeira:

a) Na equação da reta r:

3 = 2 ∙ 1 – 8

3= 2 – 8

3 = –6    (F)

A igualdade é falsa, logo o ponto não pertence à reta r.

b) Na equação da reta s:

3 = –3 ∙ 1+ 6

3 = –3 + 6

3 = 3    (V)

A igualdade é verdadeira, logo o ponto pertence à reta s.

Obviamente, que se observarmos no gráfico podemos confirmar que esses pontos pertencem ou não à cada reta:

3) Existe algum ponto que pertença às duas retas?

Observando o gráfico, obviamente, verifica-se que apenas um ponto pertence às duas retas, é exatamente onde as retas se cruzam.

Nesse caso, não é nitidamente possível saber que ponto exato essas retas se cruzam.

Para saber que ponto se cruzam, é necessário fazer algebricamente igualando as suas ordenadas inicialmente:

r: y = 2x – 8

s: y = –3x + 6

2x – 8 = –3x + 6

Feito isso, resolvemos a equação gerada e descobriremos a abscissa desse ponto de cruzamento das duas retas:

2x – 8 = –3x + 6

2x + 3x = 6 + 8

5x = 14

x = 14 / 5

x = 2,8

Obviamente, observa-se no gráfico, que os valores das coordenadas do ponto de cruzamento não são números inteiros.

A abscissa do ponto é 2,8. Para saber o valor da ordenada, basta substituir o valor na equação de qualquer uma das retas.

a) Em r: y = 2x – 8

y = 2 ∙  2,8 – 8

y = 5,6 – 8

y = –2,4

b) Em s: y = –3x + 6

y = –3 ∙ 2,8  + 6

y = –8,4 + 6

y = –2,4

De fato, o ponto de encontro terão os mesmos valores de abscissas e de ordenadas.

Portanto, nesse caso, o ponto de encontro das duas retas é (2,8; –2,4).

Logo, esse é o único ponto que pertencem às duas retas.

Atividades:

1) Escreva as equações das retas definidas pelas inclinações e interceptos abaixo.

a) Intercepto-y: 4; inclinação: −3.

b) Intercepto-y: −3; inclinação: 3.

c) Intercepto-y: 2; inclinação: 1.

d) Intercepto-y: 0; inclinação: −1.

e) Intercepto-y: −1; inclinação: 0.

 

2) Determine as equações das retas que satisfazem as condições indicadas. Em seguida, trace seus gráficos.

a) Passa por (2, −1) e tem inclinação 3.

b) Passa por (1, 5) e tem inclinação −3.

c) Passa por (−4, 8) e tem inclinação −2.

d) Passa por (0, 0) e tem inclinação 1.

e) Passa por (–1, 2) e tem inclinação 0.

 

3) Encontre as equações das retas que satisfazem as condições indicadas.

a) Passa por (−1, −3) e intercepta o eixo-y na ordenada 1. b) Passa por (1, 2) e por (2, 1).

c) Passa por (4, −2) e por (−3, −2).

d) Intercepta o eixo-y na ordenada 3 e o eixo-x na abscissa −2.

e) Intercepta o eixo-y na ordenada 2 e o eixo-x na abscissa 1.

f) Passa por (−2, −6) e intercepta o eixo-x na abscissa 10.

g) Passa por (−2, 1) e (−2, 5).

h) Passa por (4, 3) e (2, 5).

i) Reta vertical que passa por (3, −1).

j) Reta horizontal que passa por (6, −4).

 

4) Calcule a área do triângulo cujos lados estão contidos nos eixos coordenados e na reta y = −2x + 4.

 

5) Existe algum ponto em comum entre as retas r: y = 2x + 5 e s: 5x + 2 ?

 

6)  Existe algum ponto em comum entre as retas r: y = 2x – 5 e s: 2x + 3 ?

 

7) Quais dos pontos abaixo pertencem à reta de equação y = 5x – 2 ?

      (A) (1, –3)

      (B) (1, 3)

      (C) (–1, –7)

      (D) (2, 2)

 

8) Observe a representação de uma função afim no plano cartesiano abaixo.

Qual é a representação algébrica (equação da reta) dessa função?

(A) y = 4x + 2                     

(B) y = 2x + 4 

(C) y = –2x + 4                                 

(D) y = –4x+2

 

9) O gráfico, abaixo, representa uma função y = f(x) de variáveis reais.

Qual é a lei de formação (equação da reta) dessa função?

(A) y= –x/2 + 1                   

(B) y = x/2 – 2   

(C) y = –2x + 1                   

(D) y = 2x – 1

 

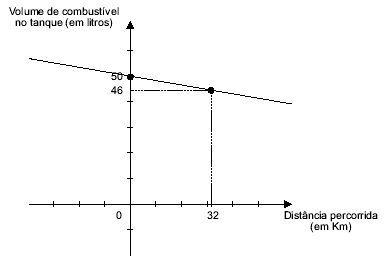
10) Ao sair para uma viagem, Paulo encheu o tanque de combustível de seu carro e, durante essa viagem, o volume de combustível variou segundo o gráfico abaixo.

A expressão que fornece o volume de combustível do carro de Paulo, em função da distância percorrida é

11) Qual dos gráficos abaixo representa a função y = – 0,5x + 4?

12) (ENEM-2011) Um bairro de uma cidade foi planejado em uma região plana, com ruas paralelas e perpendiculares, delimitando quadras de mesmo tamanho. No plano de coordenadas cartesianas seguinte, esse bairro localiza-se no segundo quadrante, e as distâncias nos eixos são dadas em quilômetros.

A reta de equação y = x + 4 representa o planejamento do percurso da linha do metrô subterrâneo que atravessará o bairro e outras regiões da cidade. No ponto P = (–5, 5), localiza-se um hospital público. A comunidade solicitou ao comitê de planejamento que fosse prevista uma estação do metrô de modo que sua distância ao hospital, medida em linha reta, não fosse maior que 5 km.

Atendendo ao pedido da comunidade, o comitê argumentou corretamente que isso seria automaticamente satisfeito, pois já estava prevista a construção de uma estação no ponto.

      (A) (–5, 0)

      (B) (–3, 1)

      (C) (–2, 1)

      (D) (0, 4)

      (E) (2, 6)

 

Equação Geral da Reta

A equação da reta pode se apresentar de diferentes formas. Uma das formas, que é bastante usual é Equação Geral da Reta, se apresentando da seguinte forma:

Ax + By + C = 0.

Sendo x e y as variáveis:

A é o coeficiente da variável x;

B é o coeficiente da variável y e

C é um coeficiente independente.

 

Como apresentar a equação reduzida da reta y = 2x – 8 na forma geral?

Nesse caso, basta colocar o y no membro onde está o coeficiente x. Assim temos: 2x – y – 8 = 0 como a equação geral da reta.

 

Exemplo: Representar na forma reduzida da seguinte equação geral da reta: 4x + 2y + 8 = 0.

Coloquemos no membro do 0 o termo com variável x e o termo independente, assim:

2y = –4x – 8

Dividindo por 2 todos os termos temos:

y = –2x – 4

Logo, y = –2x – 4 é a forma reduzida da equação geral da reta: 4x + 2y + 8 = 0.

 

Atividades:

1) Determine inclinação da reta e o coeficiente linear das equações das retas abaixo:

a) 3x + 4y – 6 = 0

b) 5x – 2y + 3 = 0

c) 2x + 3y – 12 = 0

d) 4x + y – 4 = 0

e) 5x + 7 = 0

f) 6y – 5 = 0

 

2) Ache a equação geral da reta que tem 2 como inclinação e 4 como coeficiente linear.

 

3) Verifique se o ponto A(2, 2) pertence à reta de equação 2x + 3y – 10 = 0.

 

4) Obtenha as coordenadas cartesianas do ponto comum às retas r: 2x + 3y – 12 = 0 e s: 3x + 2y – 18 = 0.

 

5) A reta t contem os pontos (4, 2) e (7, 3):

a) Determine a equação geral da reta t;

b) Determine k para que o ponto (16, k) pertença à reta t;

c) Verifique se o ponto (1997, 666) está escrito acima ou abaixo de t.

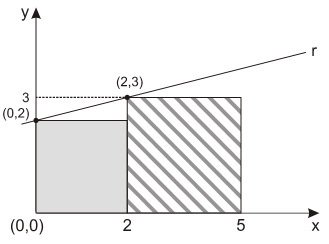
6) Na figura a seguir estão representados, em um sistema cartesiano de coordenadas, um quadrado cinza de área 4 unidades, um quadrado hachurado de área 9 unidades e a reta r que passa por um vértice de cada quadrado.

Nessas condições, a equação da reta r é:

       (A) x – 2y = –4

       (B) 4x – 9y = 0

       (C) 2x + 3y = –1

       (D) x + y = 3

       (E) 2x – y = 3

7) Um fazendeiro usa milho para produzir dois tipos de ração animal. Cada quilograma da ração A consome 0,4 kg de milho, enquanto um quilograma da ração B exige apenas 0,3 kg de milho. No momento, o fazendeiro dispõe de 10 kg de milho, que pretende usar integralmente para produzir as rações A e B.

a) Suponha que x seja a quantidade (em kg) de ração A e que y seja a quantidade de ração B que o fazendeiro pode produzir com o milho disponível. Escreva uma equação que relacione x, y e a quantidade de milho de que o fazendeiro dispõe.

b) Represente essa equação como uma reta no plano Cartesiano, considerando que x e y estão entre 0 e 40.

c) Se o fazendeiro decidir produzir 16 kg de ração A, quanto ele poderá produzir da ração B?

d) Se o fazendeiro decidir usar o milho apenas na ração A, quantos quilogramas poderá produzir?

Aprofunde-se: Outros tópicos de Geometria Analítica

Revisão: 

1) A distância entre dois pontos, C e D, de abscissas 3 e k, respectivamente, é 10. Calcule os possíveis valores de k.

 

2) Determine a distância entre os pontos (2, –1) e (–1, 3).

 

3) Calcule o perímetro, em centímetros, do triângulo de vértices A (3, 0), B (3, –7) e C (27, 0).

 

4) Dados os pontos A (–1, –1), B (5, –7) e C (x, 2), determine x sabendo que o ponto C é equidistante dos pontos A e B.

 

5) O mapa de uma região plana de uma cidade foi associado um sistema cartesiano ortogonal cuja unidade adotada nos eixos é o centímetro. Nesse sistema, cada um dos pontos, A (–2, –6) e B (13, 2) representa a localização de cada escultura. Se a escala é dada 1 : 10.000, quantos quilômetros o turista caminhou de uma escultura a outra?

 

6) No plano cartesiano, o triângulo de vértices A(1, –2) B(m, 4) e C(0, 6) é retângulo em A. Qual o valor de m?

 

7) Uma ferrovia será construída para ligar a cidade A à cidade B, que está 40 km a leste e 40 km ao sul de A.  Mas existe um lago na planície onde estão A e B, que impede a construção em linha reta. Para contornar o lago, a estrada de ferro deverá ser feita em dois trechos, passando pela cidade C, que está 35 km a leste e 28 km ao sul de A. Qual será o comprimento do trecho CB?

 

8) Calcule a área do quadrilátero ABCD, sendo A(–2, 0); B(0, –3); C(3, 0) e D(0, 4).

 

9) Qual a área do triângulo cujos lados estão contidos nos eixos coordenados e na reta de equação y = −x + 6.

 

10) Dados os pontos A(–1, 2) e B(3, –1):

 a) Marque os pontos no plano Cartesiano, considerando as abscissas no intervalo [−3,5] e as ordenadas em [−2, 3].

b) Determine a equação da reta que passa pelos pontos. Trace essa reta no gráfico.

c) Determine a ordenada do ponto dessa reta no qual a abscissa vale 1.

d) Determine a abscissa do ponto da reta que tem ordenada 0.

 

11) A reta da equação 2x + 3y – 5 = 0 intercepta o eixo y no ponto:

      (A) (0, 5)

      (B) (5/3, 0)

      (C) (0, 5/3)

      (D) (0, –5/3)

      (E) (0, 5/2)